Décomposition : tendance

Objectif

• modéliser la tendance avec différents modèles

• soustraire la tendance

• comparer les modèles

Modèles choisis

• Régression linéaire

• Régression polynomiale

• Moyenne mobile

• Moyenne mobile exponentielle

• B-Splines

Critères d’évaluation

• AIC

• MSE

• graphiquement (la courbe ne doit pas faire “n’importe quoi”)

Imports et lecture des données

Imports

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from statsmodels.graphics.tsaplots import plot_acf

from src.functions.detrend import (
    BSplinesDetrend,
    ExponentialMADetrend,
    LinearMADetrend,
    LinearRegressionDetrend,
    PolynomialRegressionDetrend,
)
from src.utils import init_notebook

init_notebook()

detrend_dict = {}

Lecture des données

data_folder = "data/raw_data"

stock_name = "AAPL"

df = pd.read_csv(
    f"{data_folder}/{stock_name}.csv", parse_dates=["Date"], index_col="Date"
)
print(f"{df.shape = }")

df.shape = (756, 6)

Soustraction de la tendance

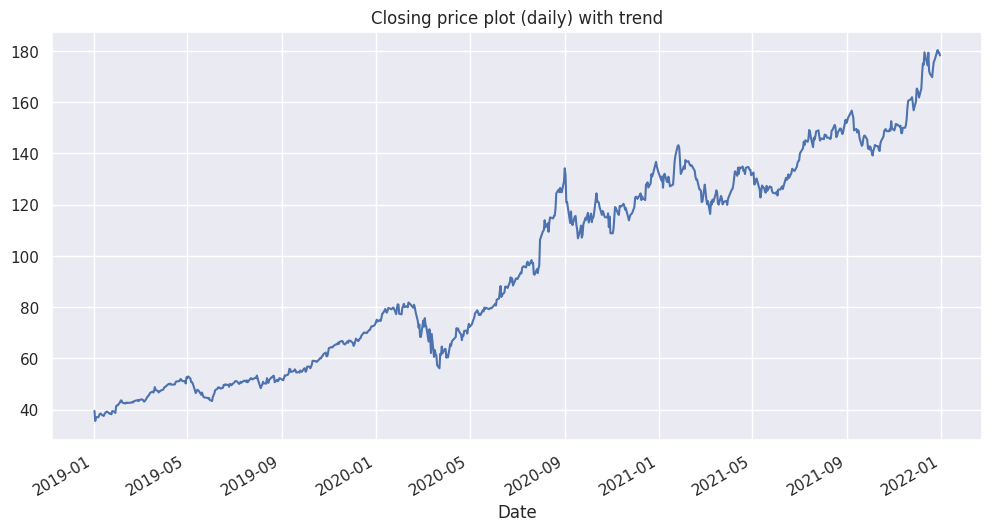
La tendance est, pour une série chronologique, sa composante première, inhérente à la nature des données. Elle peut le plus souvent se représenter par une droite, à la hausse ou à la baisse. Dans le cas des cours boursiers, le prix a une tendance généralement haussière, qui s’explique par le concept de croissance économique.

df["Close"].plot(title="Closing price plot (daily) with trend", figsize=(12, 6))

<Axes: title={'center': 'Closing price plot (daily) with trend'}, xlabel='Date'>

Régression linéaire

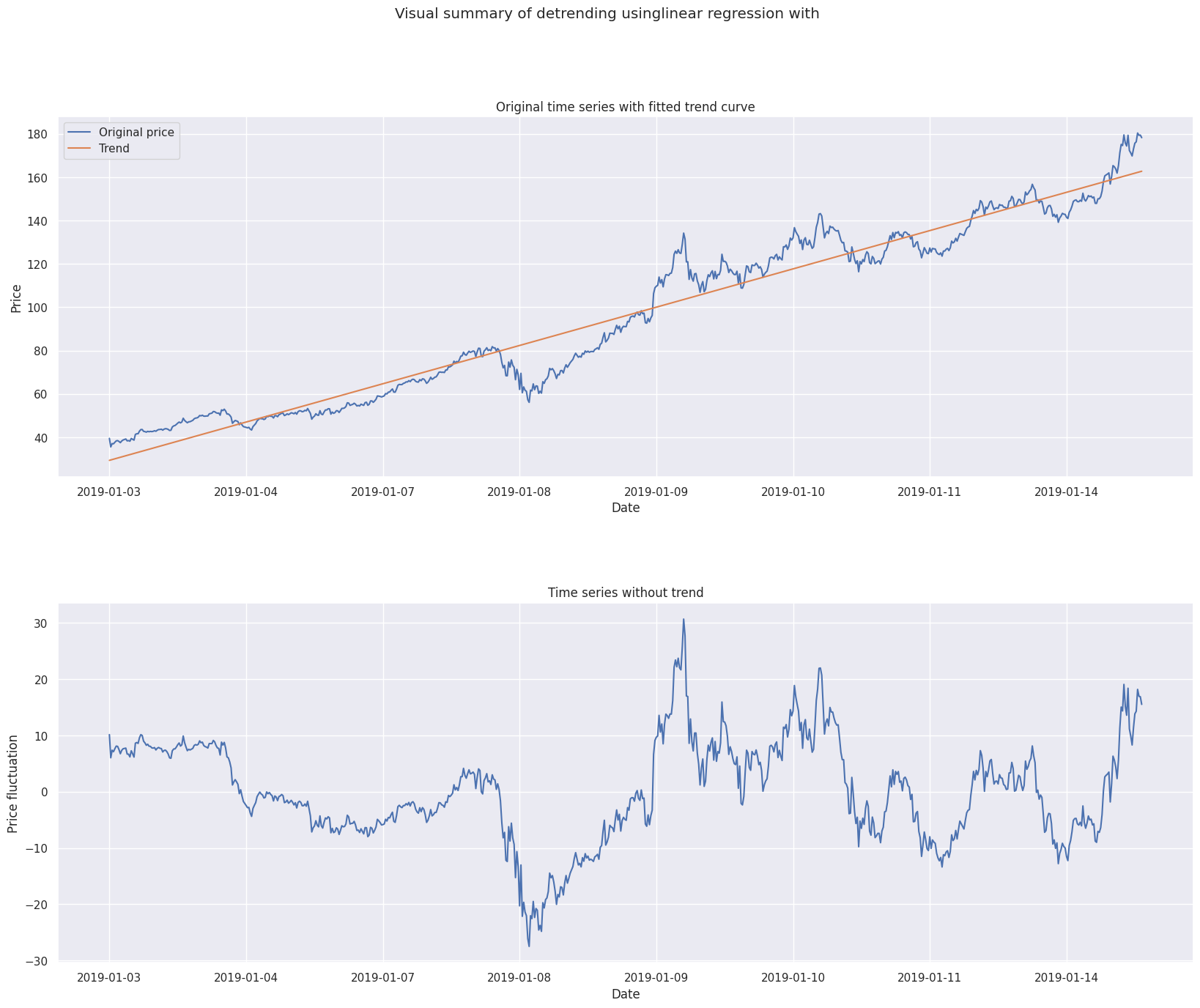
Soit le vecteur \(Y = (y_1, \dots, y_N)\) des prix de clôture du cours aux temps (ici, des jours) \(1, \dots, N\).

L’objectif est de s’ajuster aux données avec un modèle de régression linéaire simple donné par l’équation :

\[Y = \beta_0 + \beta_1 * X\]

où \((\beta_0, \beta_1)\) est le vecteur des paramètres à estimer
et \(X = (1, \dots, N)\) est le vecteur time dummy qui représente l’avancement linéaire du temps.

Puis il faut soustraire au vecteur de données originales \(Y\) le vecteur des prédictions \(Y_{pred}\) :

\[y_{detrend_i} = y_i - y_{pred_i} \hspace{12px} \forall i \in [1;N]\]

# Define time series to detrend
y = df["Close"]

# Define detrend model
detrend_model = LinearRegressionDetrend()

# Fit model to time series
y_fitted = detrend_model.fit(y)

# Substract adjusted values to original time series to get detrend data
y_detrend = detrend_model.predict(y)

# Plot the result
detrend_model.fancy_plot(xticklabels=df.index.strftime("%Y-%m-%d"))

/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:43: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[0].set_xticklabels(xticklabels)
/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:51: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[1].set_xticklabels(xticklabels)

def aic(y_true, y_detrend, nb_parameters: int) -> float:
    k = nb_parameters
    n = len(y_true)

    mse = mean_squared_error(y_true, y_detrend)
    aic = n * np.log(mse) + 2 * k

    return aic

aic_detrend = aic(y, y_detrend, 2)
mse_detrend = mean_squared_error(y, y_detrend)
detrend_dict["Régression linéaire"] = [aic_detrend, mse_detrend]

# Input detrend close price into dataframe
df["Close_detrend"] = y_detrend

# acf plot before / after

lag = len(df) - 1

_, axs = plt.subplots(2, 1, figsize=(16, 10))
_ = plot_acf(df["Close"], ax=axs[0], lags=lag, title="ACF plot - Close price")
_ = plot_acf(
    df["Close_detrend"], ax=axs[1], lags=lag, title="ACF plot - Close price detrend"
)

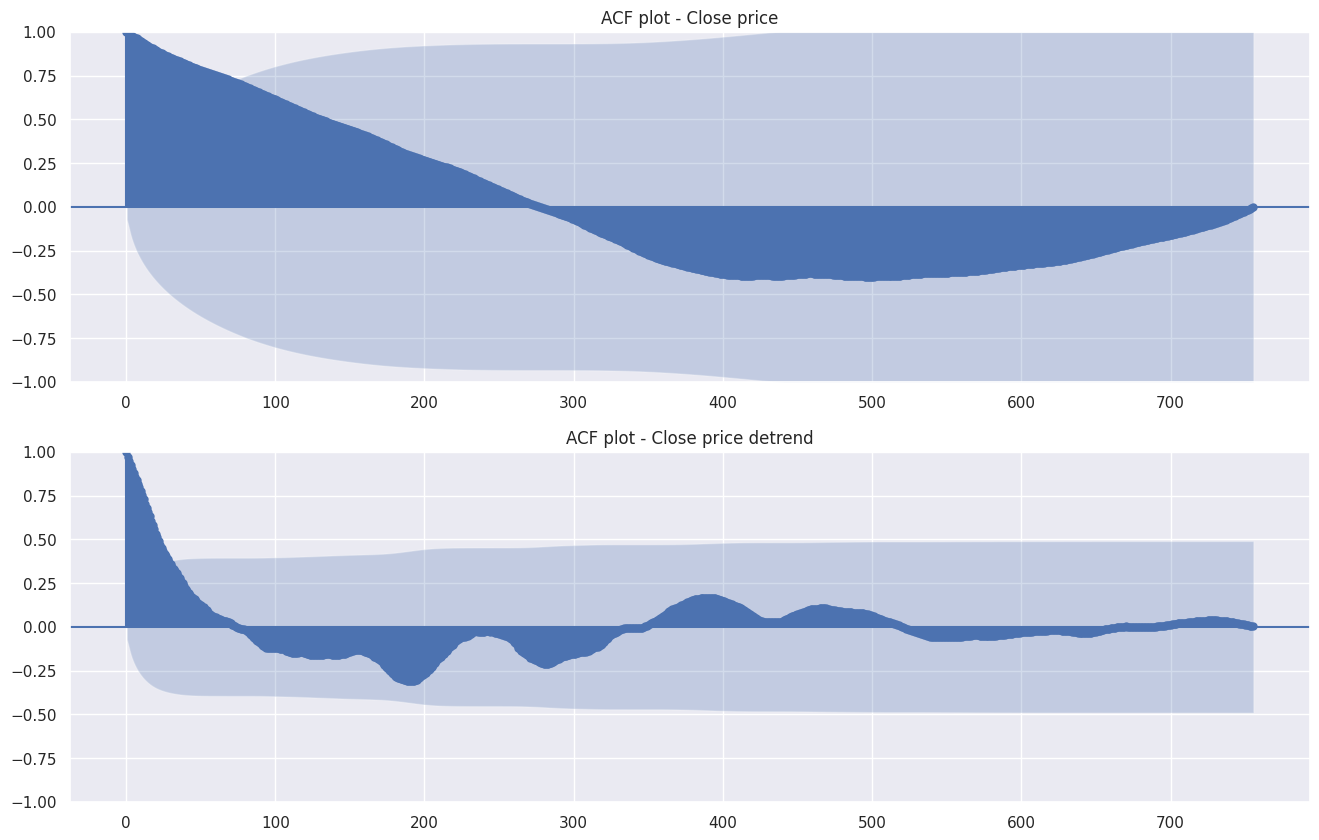
• Les fortes autocorrélations dans le premier graphique montrent que la série temporelle contient une tendance.

• Après déconstruction de la tendance, le deuxième graphique affiche cependant encore des autocorrélations importantes pour des lags petits. C’est un indice de saisonnalité ou de cyclicité.

Régression polynomiale par morceaux

Soit \(k \in N^*\).
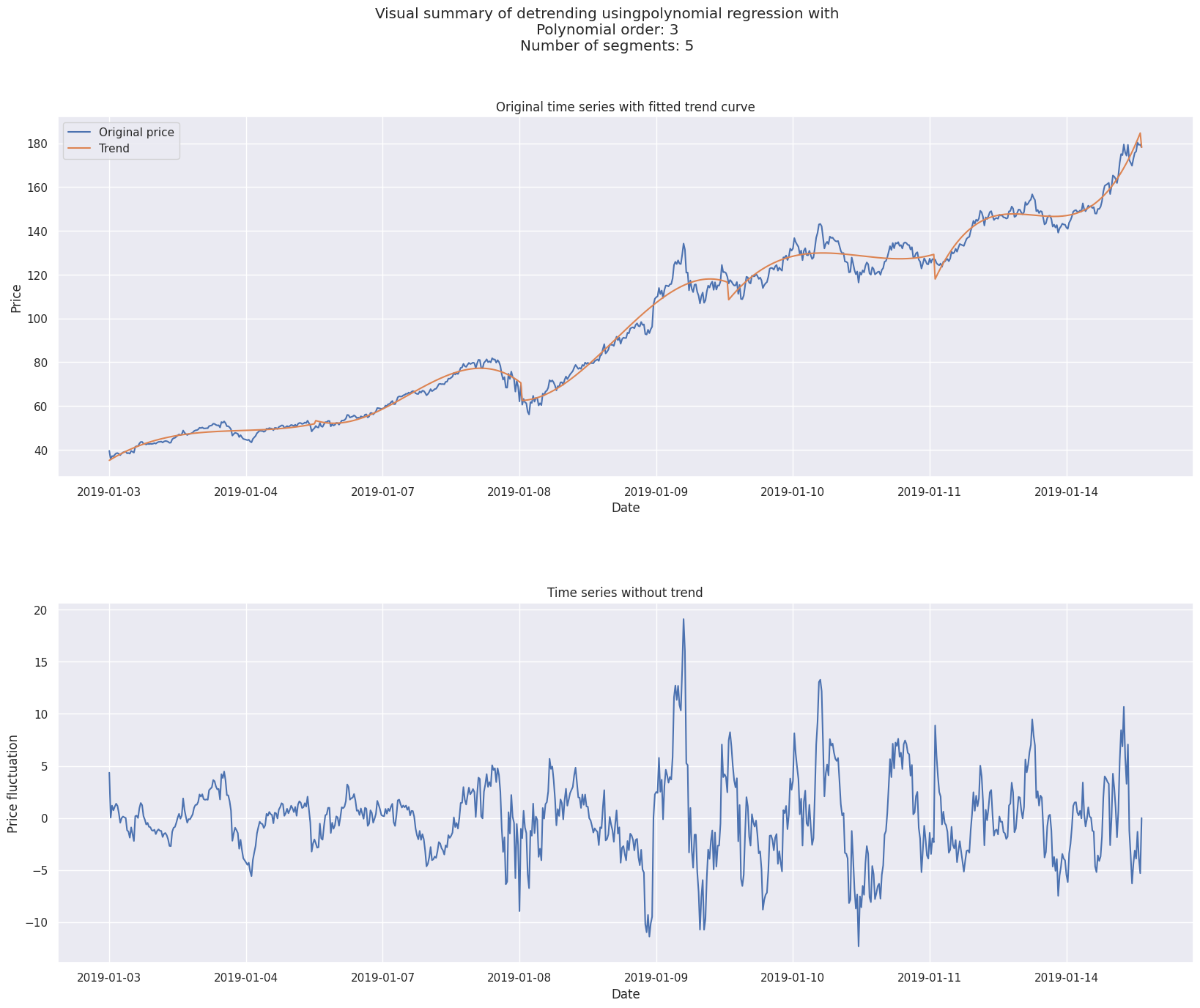
Pour la régression polynomiale d’ordre \(k\), le même principe que la régression linéaire simple est appliqué mais avec la particularité que des time dummies d’ordre \(1, \dots, k\) sont ajoutées comme variables explicatives au modèle.
L’équation de régression devient :

\[ Y = \sum_{i=0}^{k} \beta_i * X_i\]

où pour tout \(i \in [1;k], \hspace{6px} X_i = (1^i, 2^i, \dots, N^i)\).

Cette méthode permet de capter une tendance polynomiale (croissante au carré du temps par exemple).

# Choose parameters of segmented polynomial regression

order = 3
n_segments = 5

# Define detrend model
detrend_model = PolynomialRegressionDetrend(order=order, n_segments=n_segments)

# Fit model to time series
y_fitted = detrend_model.fit(y)

# Substract adjusted values to original time series to get detrend data
y_detrend = detrend_model.predict(y)

# Plot the result
detrend_model.fancy_plot(xticklabels=df.index.strftime("%Y-%m-%d"))

/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:43: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[0].set_xticklabels(xticklabels)
/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:51: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[1].set_xticklabels(xticklabels)

aic_detrend = aic(y, y_detrend, 2)
mse_detrend = mean_squared_error(y, y_detrend)
detrend_dict["Régression polynomiale"] = [aic_detrend, mse_detrend]

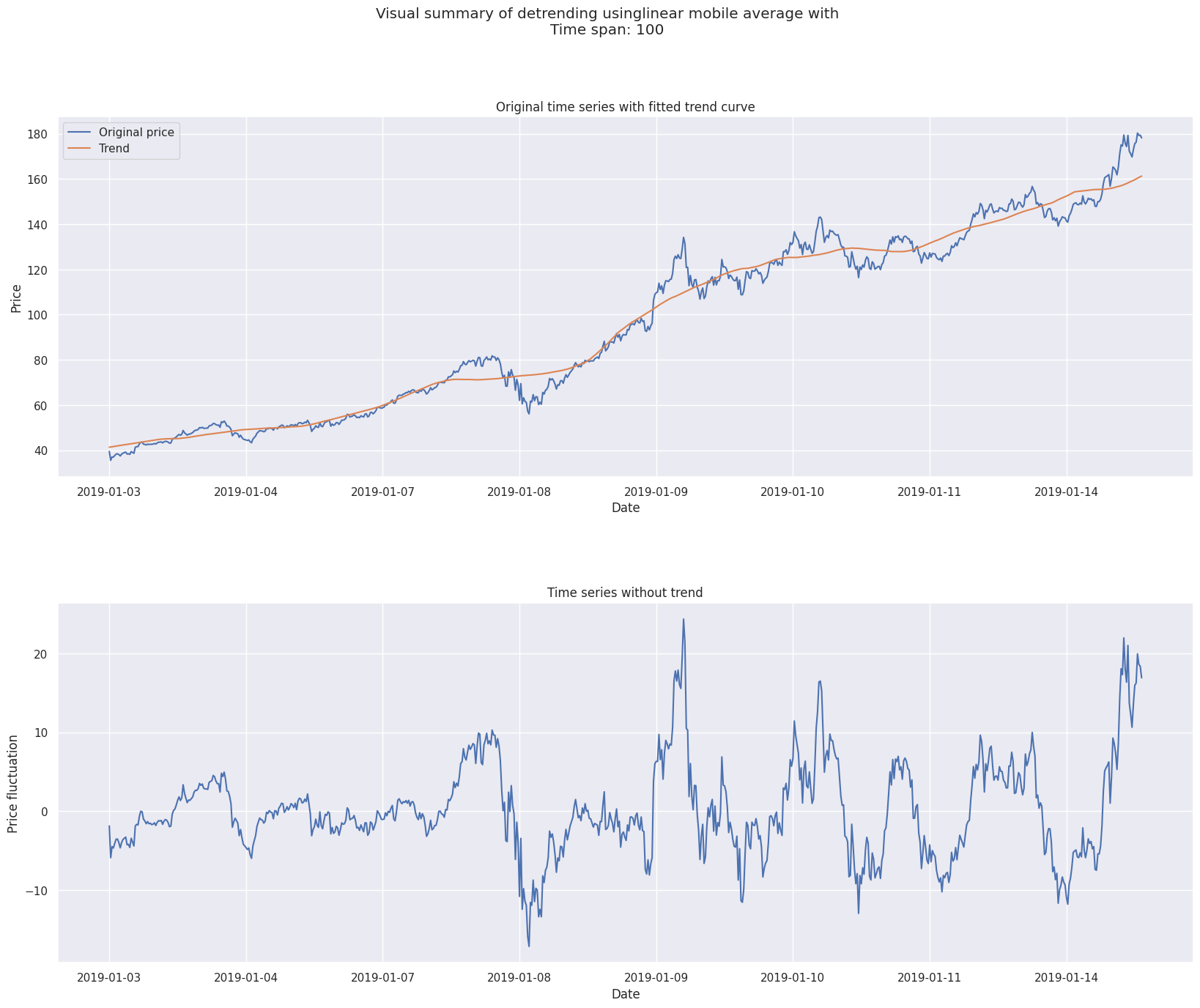
Moyennes mobiles

Linéaire

On se munit de \((x_t)_{t \in \mathbb{N}}\) une série temporelle.

Soit \((k, t) \in \mathbb{N}^* \times \llbracket k~;~+\infty \rrbracket\),
la moyenne mobile linéaire à gauche de profondeur \(k\) pour \(x_t\) est :

\[ma_k(x_t) = \frac{\displaystyle \sum_{i=t-k+1}^{t}x_i}{k}\]

# Define detrend model
detrend_model = LinearMADetrend(window=100)

# Fit model to time series
y_fitted = detrend_model.fit(y)

# Substract adjusted values to original time series to get detrend data
y_detrend = detrend_model.predict(y)

# Plot the result
detrend_model.fancy_plot(xticklabels=df.index.strftime("%Y-%m-%d"))

/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:43: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[0].set_xticklabels(xticklabels)
/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:51: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[1].set_xticklabels(xticklabels)

aic_detrend = aic(y, y_detrend, 2)
mse_detrend = mean_squared_error(y, y_detrend)
detrend_dict["Moyenne mobile linéaire"] = [aic_detrend, mse_detrend]

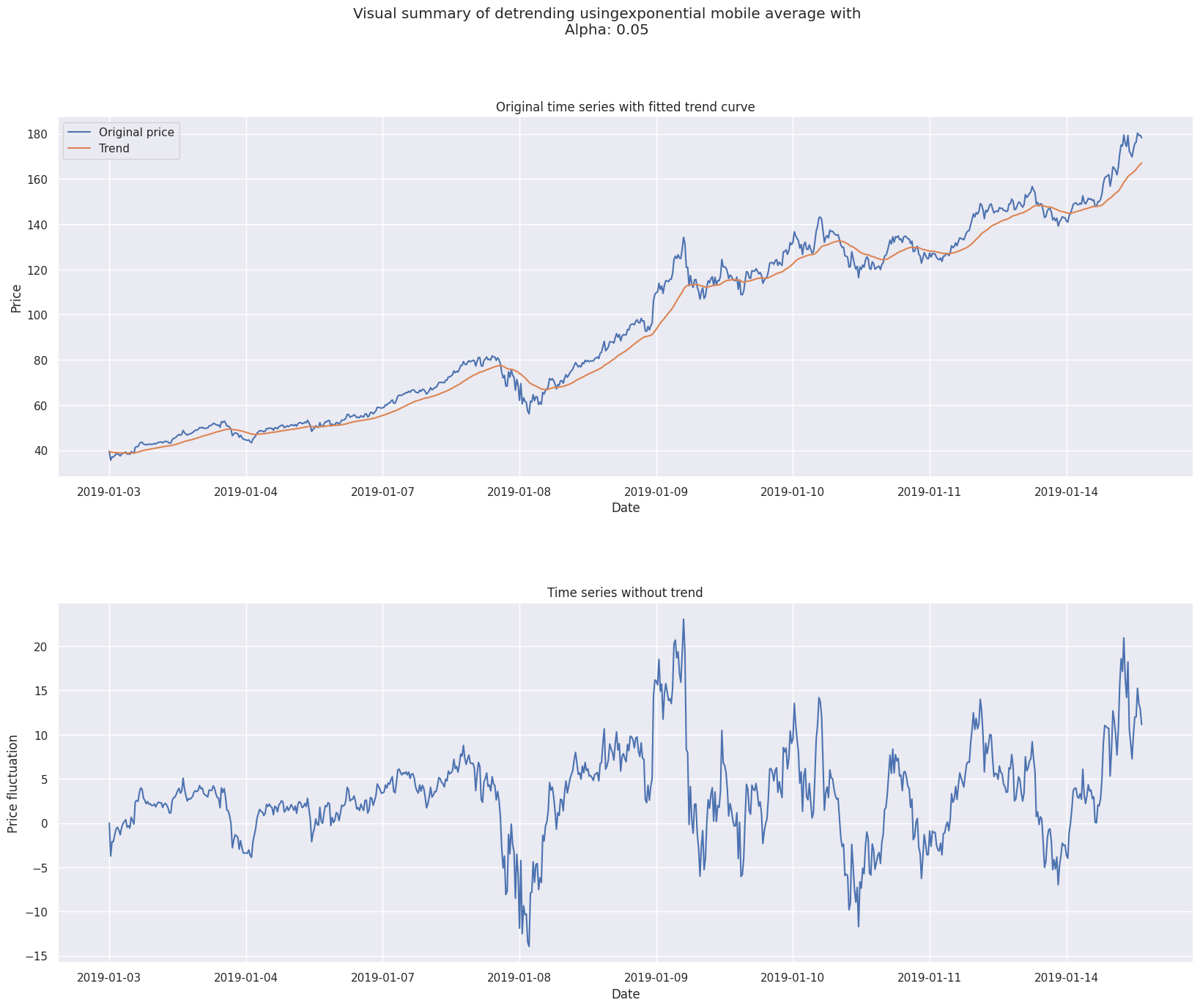
Exponentielle

La moyenne mobile exponentielle fait partie de la famille des moyennes mobiles pondérées.

On se munit de \((x_t)_{t \in \mathbb{N}}\) une série temporelle.

Soit \(t \in \mathbb{N}^*\) et \(\alpha \in [0;1]\) une constante de lissage.

\[\begin{split} \begin{align} expma(x_{t}) & = \alpha \left ( x_t + (1 - \alpha) x_{t - 1} + (1 - \alpha)^2 x_{t-2} + (1 - \alpha)^3 x_{t - 3} + \dots \right ) \\ & = \displaystyle\sum_{n = 0}^{t} \alpha(1 - \alpha)^n x_{t - n} \end{align} \end{split}\]

On remarque que la moyenne mobile exponentielle à l’instant \(t\) prend en compte toutes les données qui précèdent. Toutefois, les valeurs très antérieures impactent très peu le résultat - d’autant plus que \(\alpha\) est grand - et peuvent donc être négligées.

# Define detrend model
detrend_model = ExponentialMADetrend(alpha=0.05)

# Fit model to time series
y_fitted = detrend_model.fit(y)

# Substract adjusted values to original time series to get detrend data
y_detrend = detrend_model.predict(y)

# Plot the result
detrend_model.fancy_plot(xticklabels=df.index.strftime("%Y-%m-%d"))

/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:43: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[0].set_xticklabels(xticklabels)
/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:51: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[1].set_xticklabels(xticklabels)

aic_detrend = aic(y, y_detrend, 2)
mse_detrend = mean_squared_error(y, y_detrend)
detrend_dict["Moyenne mobile exponentielle"] = [aic_detrend, mse_detrend]

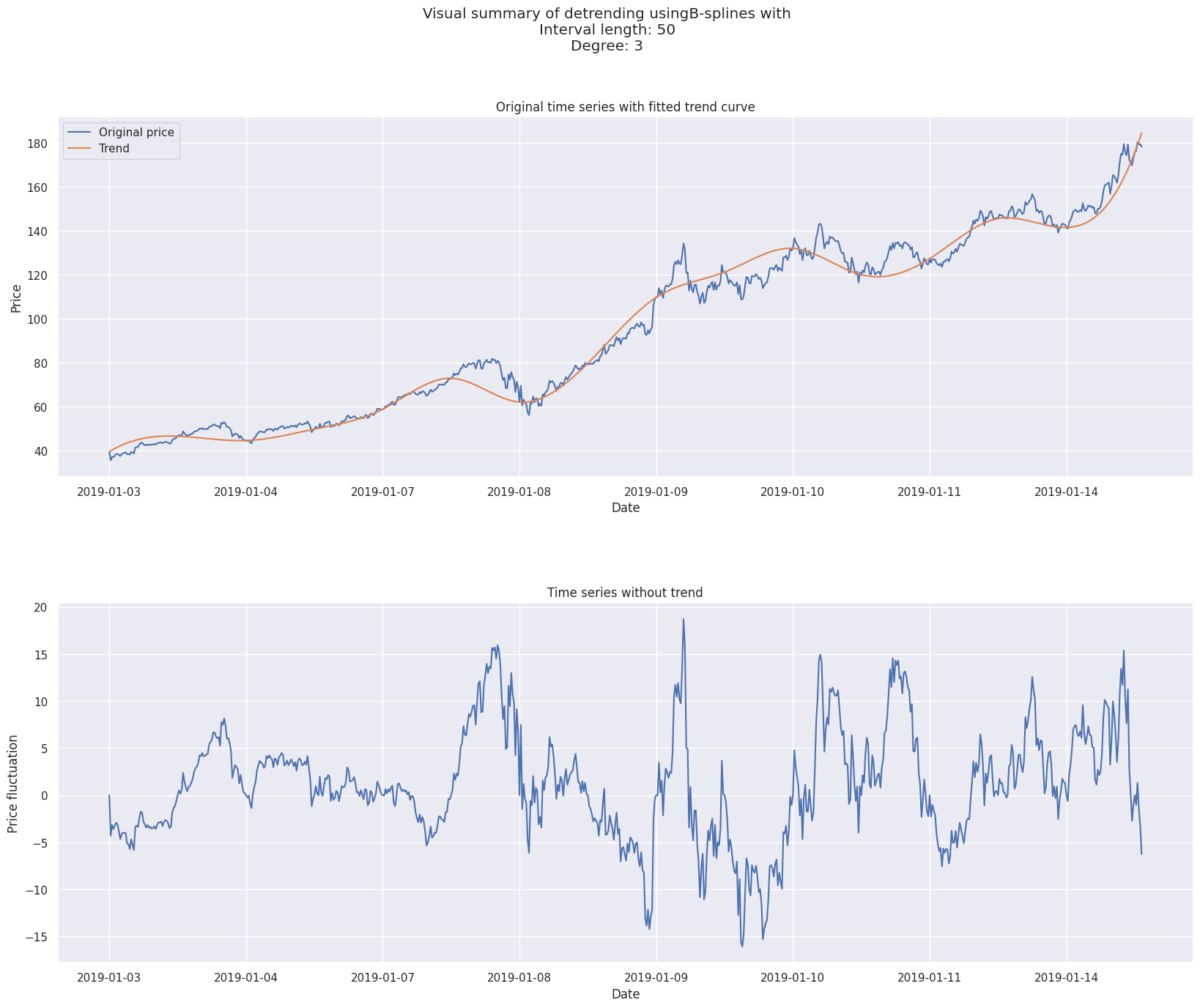
B-splines

Étant donné \(m + 1\) nœuds \( \{t_i \in [0, 1]\}_{i \in [0, m]} \) indexés selon le temps,
une courbe spline de degré \(n \in \mathbb{N^*}\) est une fonction paramétrique définie par :

\[ \mathbf{S} \,:\, [0,1] \to \mathbb{R}^d\]

\[\begin{split} S : \begin{cases} \mathbb{[0, 1]} & \rightarrow \mathbb{R}^2 \\ t & \rightarrow \displaystyle \sum_{i = 0}^{m - n - 1} b_{i, n} (t) . \mathbf{P}_{i} * \mathbb{1}_{t \in [t_{n}, t_{m-n}]} \end{cases} \end{split}\]

Les B-splines sont des fonctions utilisées pour l’interpolation ou l’approximation de fonctions continues à partir de données discrètes.

\(\forall k \in \mathbb{N^*}\), la fonction B-spline de degré k, notée \(B_{i, k}(t)\), est définie récursivement comme suit :

\[\begin{split} B_{i,0}(t) = \begin{cases} 1 & \text{si } t_i \leq t < t_{i+1} \\ 0 & \text{sinon} \end{cases} \end{split}\]

\[ B_{i,k}(t) = \frac{t - t_i}{t_{i+k} - t_i} B_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i+k+1} - t_{i+1}} B_{i+1,k-1}(t) \]

Pour \( i \in {0,1,…,n−k−2}\), où \(n\) est le nombre total de points de contrôle et \(k\) est l’ordre des B-splines.

# Define parameters for B-splines

interval_length = 50  # Days between two knots
degree = 3

# Define detrend model
detrend_model = BSplinesDetrend(interval_length=interval_length, degree=degree)

# Fit model to time series
y_fitted = detrend_model.fit(y)

# Substract adjusted values to original time series to get detrend data
y_detrend = detrend_model.predict(y)

# Plot the result
detrend_model.fancy_plot(xticklabels=df.index.strftime("%Y-%m-%d"))

/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:43: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[0].set_xticklabels(xticklabels)
/home/runner/work/stock-analysis/stock-analysis/src/functions/detrend_fancy_plot.py:51: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  axs[1].set_xticklabels(xticklabels)

aic_detrend = aic(y, y_detrend, 2)
mse_detrend = mean_squared_error(y, y_detrend)
detrend_dict["B-Splines"] = [aic_detrend, mse_detrend]

La méthode des BSplines de degré 1 correspond à de l’interpolation linéaire :

detrend_df = pd.DataFrame(detrend_dict).T
detrend_df.columns = ["AIC", "MSE"]
detrend_df["Graphiquement"] = "✅"

# print(detrend_df.to_markdown())

detrend_df[["AIC", "MSE"]].plot(kind="bar")
plt.title("Comparaison des modèles de tendance")

plt.xticks(rotation=45, ha="right")

(array([0, 1, 2, 3, 4]),
 [Text(0, 0, 'Régression linéaire'),
  Text(1, 0, 'Régression polynomiale'),
  Text(2, 0, 'Moyenne mobile linéaire'),
  Text(3, 0, 'Moyenne mobile exponentielle'),
  Text(4, 0, 'B-Splines')])

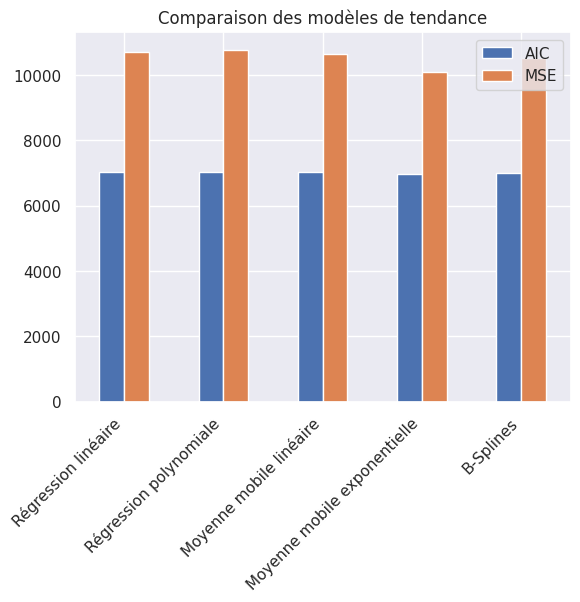
Tableau. Comparaison des modèles de tendance

	AIC	MSE	Graphiquement
Régression linéaire	7005.56	10523.1	✅
Régression polynomiale	7023.09	10770	✅
Moyenne mobile linéaire	7014.76	10651.8	✅
Moyenne mobile exponentielle	6973.26	10082.9	✅
B-Splines	7005.56	10523.1	✅

Meilleur modèle : moyenne mobile exponentielle