Régression (v1)#
Import des outils / jeu de données#
1import statistics
2
3import matplotlib.pyplot as plt
4import numpy as np
5import pandas as pd
6import seaborn as sns
7import statsmodels.api as sm
8import statsmodels.stats.api as sms
9import xgboost
10from keras import layers
11from scipy import stats
12from scipy.stats import kstest, pearsonr, poisson
13from sklearn.cross_decomposition import PLSRegression
14from sklearn.linear_model import LinearRegression, PoissonRegressor
15from sklearn.metrics import mean_absolute_error, mean_squared_error
16from sklearn.model_selection import train_test_split
17from sklearn.preprocessing import PolynomialFeatures
18from statsmodels.compat import lzip
19from statsmodels.graphics.regressionplots import *
20from statsmodels.stats.outliers_influence import variance_inflation_factor
21from tensorflow import keras
22
23from src.config import data_folder
24from src.constants import var_categoriques, var_numeriques
25from src.utils import init_notebook
2023-12-17 21:40:17.874455: I external/local_tsl/tsl/cuda/cudart_stub.cc:31] Could not find cuda drivers on your machine, GPU will not be used.
2023-12-17 21:40:17.904062: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered
2023-12-17 21:40:17.904097: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered
2023-12-17 21:40:17.905286: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
2023-12-17 21:40:17.911163: I external/local_tsl/tsl/cuda/cudart_stub.cc:31] Could not find cuda drivers on your machine, GPU will not be used.
2023-12-17 21:40:17.912274: I tensorflow/core/platform/cpu_feature_guard.cc:182] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.
2023-12-17 21:40:21.024366: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT
1init_notebook()
1df = pd.read_csv(
2 f"{data_folder}/data-cleaned-feature-engineering.csv",
3 sep=",",
4 index_col="ID",
5 parse_dates=True,
6)
1df_transforme = pd.read_csv(
2 f"{data_folder}/data-transformed.csv",
3 sep=",",
4 index_col="ID",
5 parse_dates=True,
6)
Variables globales#
Fonctions et variables utiles#
1score_modeles = []
1def affiche_score(modele, y_test, y_pred):
2 """Affiche la MSE, RMSE et MAE du modèle."""
3 print(f"MSE = {mean_squared_error(y_test, y_pred)}")
4 print(f"RMSE = {mean_squared_error(y_test, y_pred, squared=False)}")
5 print(f"MAE = {mean_absolute_error(y_test, y_pred)}")
1def ajout_score(modele, nom_modele, y_test, y_pred):
2 """Ajoute la MMSE, RMSE et MAE au dataframe score_modeles."""
3 score_modeles.extend(
4 (
5 [nom_modele, "mse", mean_squared_error(y_test, y_pred)],
6 [nom_modele, "rmse", mean_squared_error(y_test, y_pred, squared=False)],
7 [nom_modele, "mae", mean_absolute_error(y_test, y_pred)],
8 )
9 )
Régression linéaire simple#
Modèle simple : une variable à expliquer $Y$ et une seule variable explicative $X$.
$$y_i = \beta_0 + \beta_1 X_i + \epsilon_i$$
Hypothèses à vérifier pour la régression linéaire simple :
il existe une corrélation linéaire entre $X$ et $Y$
la distribution de l’erreur $\epsilon$ est indépendante de la variable X (exogénéité)
l’erreur suit une loi normale centrée i.e. $E(ε_i) = 0$
l’erreur est de variance constante (homoscédasticité) i.e $Var(ε_i) = \sigma^2$, une constante
les erreurs sont indépendantes (absence d’autocorrélation) i.e. $Cov(εi, εj) = 0$, pour tout $i, j \in N \times N, i \neq j$
1X = np.array(df_transforme["Income"])
2Y = np.array(df_transforme["NumStorePurchases"])
Hypothèse 1 : corrélation linéaire#
1print(
2 "Le coefficient de corrélation linéaire entre X et Y vaut",
3 pearsonr(X, Y)[0],
4 "la pvalue associée vaut",
5 pearsonr(X, Y)[1],
6 "il existe donc bien une relation linéaire entre X et Y.",
7)
Le coefficient de corrélation linéaire entre X et Y vaut 0.6790710752806047 la pvalue associée vaut 1.3161539637560999e-276 il existe donc bien une relation linéaire entre X et Y.
Le reste des hypothèses à tester requiert d’effectuer la régression linéaire :
1X_train, X_test, Y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
1model = LinearRegression().fit(X_train.reshape(-1, 1), Y_train)
2Y_train_hat = model.predict(X_train.reshape(-1, 1))
1plt.scatter(X_train, Y_train, color="black")
2plt.plot(X_train, Y_train_hat, color="red")
3plt.title("Régression linéaire du nombre d'achats en magasin en fonction du revenu")
Text(0.5, 1.0, "Régression linéaire du nombre d'achats en magasin en fonction du revenu")
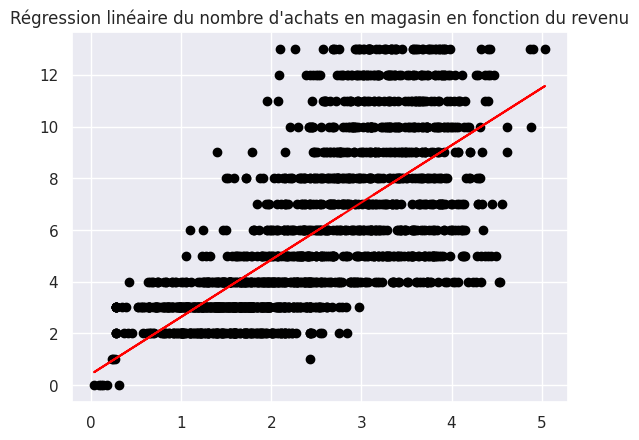
1print(model.intercept_, model.coef_, model.score(X_train.reshape(-1, 1), Y_train))
0.41932027328891675 [2.21369643] 0.47029950823152755
Equation de régression :
$$y_i = 0.42 + 2.21 * x_i$$
Hypothèse 2 : exogénéité#
1residuals = Y_train - Y_train_hat
2
3plt.scatter(X_train, residuals)
<matplotlib.collections.PathCollection at 0x7f95055e3b50>
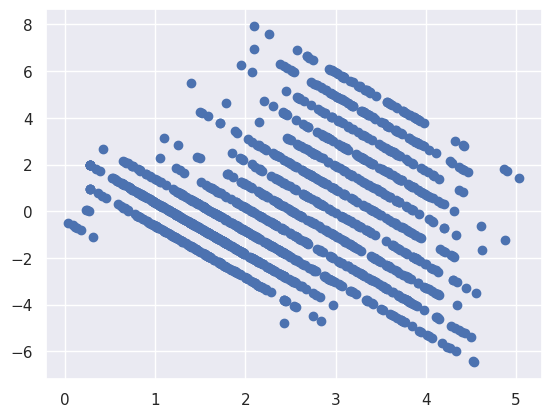
1print(
2 "Le coefficient de corrélation entre X et les residus vaut",
3 pearsonr(X_train, residuals)[0],
4 ". On a bien indépendance et donc exogénéité.",
5)
Le coefficient de corrélation entre X et les residus vaut -2.8216361538935253e-16 . On a bien indépendance et donc exogénéité.
Hypothèse 3 : l’erreur suit une loi normale centrée i.e. E(ε_i) = 0#
1plt.hist(residuals, density=True)
2
3x = np.linspace(-7, 7, 100)
4plt.plot(x, stats.norm.pdf(x, 0, 1))
5plt.title("Histogramme des résidus en superposition avec la densité de la loi normale")
6plt.show()
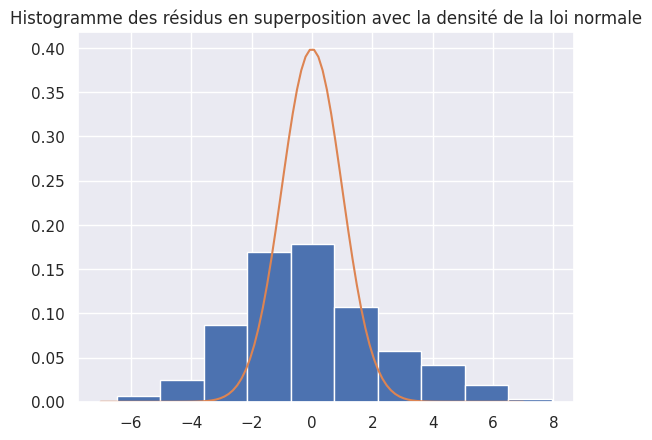
1print("La moyenne des résidus vaut", statistics.mean(residuals))
2print("Mais les résidus ne suivent pas une loi normale")
La moyenne des résidus vaut -5.35770830037629e-16
Mais les résidus ne suivent pas une loi normale
1sm.qqplot(residuals, line="45")
2print("On constate sur le qqplot que les points ne suivent pas la droite x = y")
On constate sur le qqplot que les points ne suivent pas la droite x = y
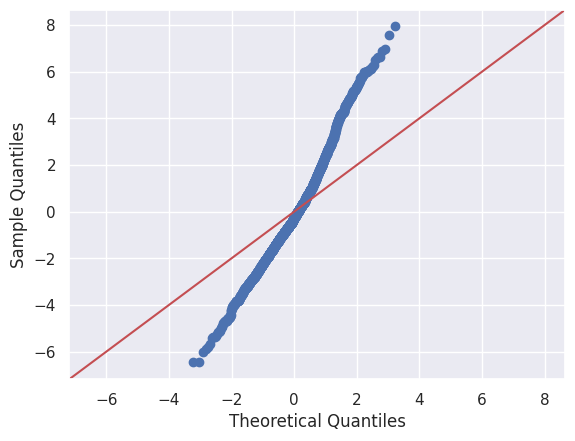
1print(
2 "Un test de shapiro, pour tester l'hypothèse de normalité, nous donne une pvalue de",
3 stats.shapiro(residuals)[1],
4 ". On rejette l'hypothèse nulle et on conclut que les résidus ne suivent pas une loi normale.",
5)
Un test de shapiro, pour tester l'hypothèse de normalité, nous donne une pvalue de 1.5231739480814355e-12 . On rejette l'hypothèse nulle et on conclut que les résidus ne suivent pas une loi normale.
Hypothèse 4 : homoscédasticité#
1def abline(slope, intercept):
2 axes = plt.gca()
3 x_vals = np.array(axes.get_xlim())
4 y_vals = intercept + slope * x_vals
5 plt.plot(x_vals, y_vals, "-", color="red")
1plt.plot(residuals, "bo")
2plt.title("Nuage de points des résidus")
3abline(0, 7)
4abline(0, -7)
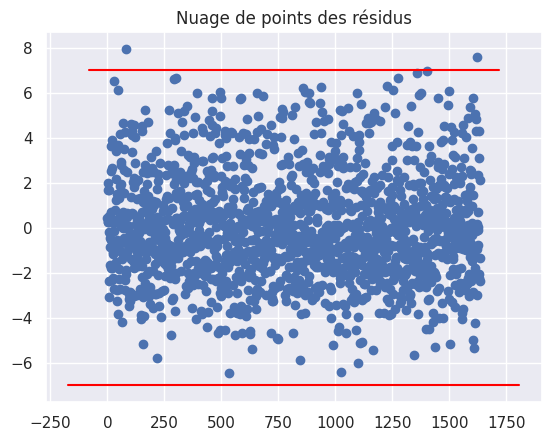
1fit = sm.OLS(Y_train, sm.add_constant(X_train)).fit()
1fit.summary()
| Dep. Variable: | y | R-squared: | 0.470 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.470 |
| Method: | Least Squares | F-statistic: | 1451. |
| Date: | Sun, 17 Dec 2023 | Prob (F-statistic): | 9.81e-228 |
| Time: | 21:40:24 | Log-Likelihood: | -3726.4 |
| No. Observations: | 1636 | AIC: | 7457. |
| Df Residuals: | 1634 | BIC: | 7468. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.4193 | 0.153 | 2.738 | 0.006 | 0.119 | 0.720 |
| x1 | 2.2137 | 0.058 | 38.089 | 0.000 | 2.100 | 2.328 |
| Omnibus: | 51.217 | Durbin-Watson: | 2.019 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 55.343 |
| Skew: | 0.447 | Prob(JB): | 9.60e-13 |
| Kurtosis: | 3.105 | Cond. No. | 7.78 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
1res_names = ["F statistic", "p-value"]
2gq_test = sms.het_goldfeldquandt(fit.resid, fit.model.exog)
3lzip(res_names, gq_test)
[('F statistic', 1.0633264046598987), ('p-value', 0.19033564154336408)]
1bp_test = sms.het_breuschpagan(fit.resid, fit.model.exog)
2lzip(res_names, bp_test)
[('F statistic', 222.40463115768435), ('p-value', 2.7032416707307303e-50)]
Le test de Goldfeld-Quandt ne nous donne pas d’hétéroscédasticité, contraiement au test de Breusch-Pagan.
Hypothèse 5 : absence d’autocorrélation#
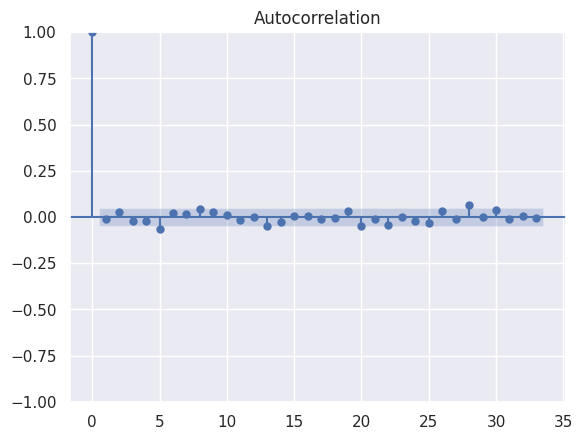
1sm.graphics.tsa.plot_acf(residuals)
2print("On remarque une absence d'autocorrélation.")
On remarque une absence d'autocorrélation.
Distance de Cook#
1influence = fit.get_influence()
2cooks = influence.cooks_distance
1plt.scatter(X_train, cooks[0])
2plt.xlabel("Revenus")
3plt.ylabel("Distances de Cook")
4plt.show()
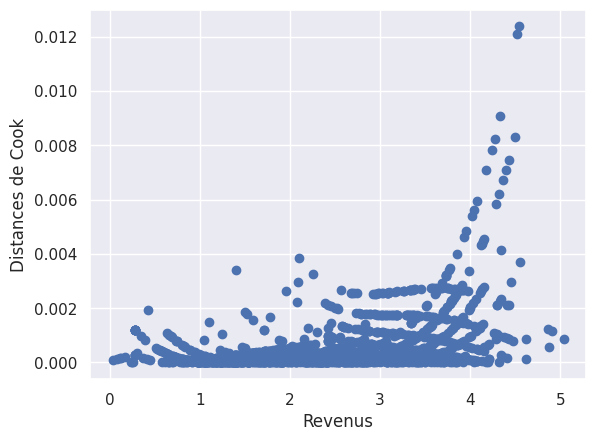
1cooks_indexes = [i for i, x in enumerate(cooks[0] > 0.010) if x]
2print(cooks_indexes)
3## affiche les indexes des individus dont les distances de cook dépassent une certaine valeur
[532, 1026]
1influence_plot(fit)
2print("")
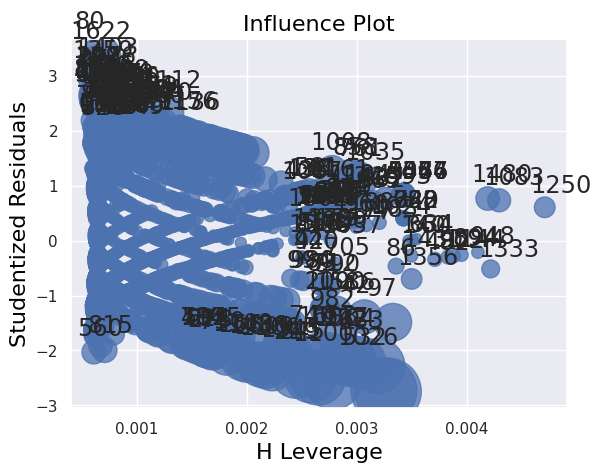
Score du modèle#
Qualité d’ajustement#
1print(f"Le R² du modèle vaut {model.score(X_train.reshape(-1, 1), Y_train)}")
Le R² du modèle vaut 0.47029950823152755
1print(f"MSE = {mean_squared_error(Y_train, Y_train_hat)}")
2print(f"RMSE = {mean_squared_error(Y_train, Y_train_hat, squared=False)}")
3print(f"MAE = {mean_absolute_error(Y_train, Y_train_hat)}")
MSE = 5.571127360403869
RMSE = 2.3603235711240673
MAE = 1.8519616230655271
Qualité de prédiction#
Train / test split
1print(
2 f"R² du modèle sur les données d'entraînement = {model.score(X_train.reshape(-1, 1), Y_train)}"
3)
4print(
5 f"R² du modèle sur les données de test = {model.score(X_test.reshape(-1, 1), y_test)}"
6)
R² du modèle sur les données d'entraînement = 0.47029950823152755
R² du modèle sur les données de test = 0.4225134353582901
1y_pred = model.predict(X_test.reshape(-1, 1))
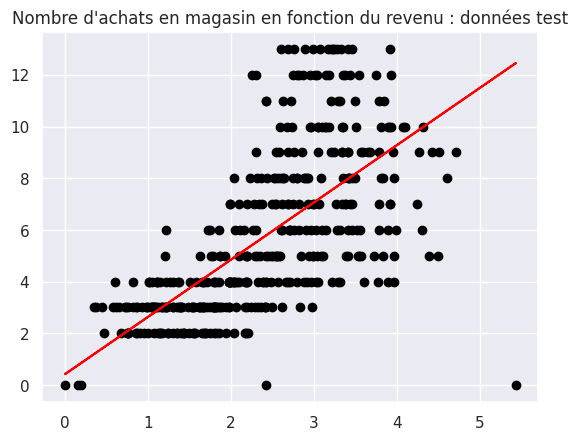
1plt.scatter(X_test, y_test, color="black")
2plt.plot(X_test, y_pred, color="red")
3plt.title("Nombre d'achats en magasin en fonction du revenu : données test")
Text(0.5, 1.0, "Nombre d'achats en magasin en fonction du revenu : données test")
1affiche_score(model, y_test, y_pred)
MSE = 5.853872571999743
RMSE = 2.419477747779413
MAE = 1.8268826341039772
1nom_modele = "Régression simple"
2ajout_score(model, nom_modele, y_test, y_pred)
1## todo: cross-validation
Régression linéaire multiple#
Modèle multiple : une variable à expliquer $Y$ et $P$ variables explicatives $X_i$
$$y_i = \beta_0 + \beta_1 X_i(1) + \beta_2 X_i(2) + \beta_3 X_i(3) + … + \beta_P X_i(P) + \epsilon_i$$
Hypothèses à vérifier pour la régression linéaire multiple :
il existe une corrélation linéaire entre $X_i$ et $Y$
$Cov(X_i, ε_j) = 0$, pour tout $i, j \in N \times N, i \neq j$ (exogénéité) et pour chaque variable explicative $X_p$
l’erreur suit une loi normale centrée i.e. $E(ε_i) = 0$
l’erreur est de variance constante (homoscédasticité) i.e $Var(ε_i) = \sigma^2$, une constante
les erreurs sont indépendantes (absence d’autocorrélation) i.e. $Cov(εi, εj) = 0$, pour tout $i, j \in N \times N, i \neq j$
absence de colinéarité entre les variables explicatives, i.e. $X^t * X$ est régulière, $det(X^t * X) \neq 0$
Pour les besoins de la régression linéaire, nous créons des variables muettes (dummy variables) pour inclure les variables catégoriques Education et Marital_status à la régression.
1df_reg = df_transforme.copy()
1df_reg = pd.get_dummies(df_reg, columns=["Education", "Marital_Status"])
1df_reg.columns
Index(['Year_Birth', 'Income', 'Kidhome', 'Teenhome', 'Dt_Customer', 'Recency',
'MntWines', 'MntFruits', 'MntMeatProducts', 'MntFishProducts',
'MntSweetProducts', 'MntGoldProds', 'NumDealsPurchases',
'NumWebPurchases', 'NumCatalogPurchases', 'NumStorePurchases',
'NumWebVisitsMonth', 'AcceptedCmp3', 'AcceptedCmp4', 'AcceptedCmp5',
'AcceptedCmp1', 'AcceptedCmp2', 'Complain', 'Response',
'NbAcceptedCampaigns', 'HasAcceptedCampaigns', 'NbChildren',
'Education_2n Cycle', 'Education_Basic', 'Education_Graduation',
'Education_Master', 'Education_PhD', 'Marital_Status_Divorced',
'Marital_Status_Married', 'Marital_Status_Single',
'Marital_Status_Together', 'Marital_Status_Widow'],
dtype='object')
Pour cette régression, on suppose que l’entreprise veut profiler au mieux les clients qui achètent dans le magasin. C’est pourquoi la variable d’intérêt pour la régression sera le nombre d'achats en magasin.
Nos variables explicatives sont des variables numériques et des variables catégoriques transformées en variables muettes. Nous commençons par un grand nombre de variables explicatives puis nous en éliminerons progressivement pendant la vérifications des hypothèses.
1var_numeriques_reg = [
2 "Income",
3 "Year_Birth",
4 "Recency",
5 "NbAcceptedCampaigns",
6 "NumWebPurchases",
7 "NumDealsPurchases",
8 "NumWebVisitsMonth",
9 "NumCatalogPurchases",
10 "MntWines",
11 "MntFruits",
12 "MntMeatProducts",
13 "MntFishProducts",
14 "MntSweetProducts",
15 "MntGoldProds",
16]
17
18var_categoriques_reg = [
19 "NbChildren",
20 "Education_2n Cycle",
21 "Education_Basic",
22 "Education_Graduation",
23 "Education_Master",
24 "Education_PhD",
25 "Marital_Status_Divorced",
26 "Marital_Status_Married",
27 "Marital_Status_Single",
28 "Marital_Status_Together",
29 "Marital_Status_Widow",
30]
1X = df_reg[var_categoriques_reg + var_numeriques_reg]
2Y = df_reg["NumStorePurchases"]
1print(
2 "Nous avons",
3 X.shape[1],
4 "variables explicatives au début de la régression dont",
5 X[var_numeriques_reg].shape[1],
6 "variables numériques.",
7)
Nous avons 25 variables explicatives au début de la régression dont 14 variables numériques.
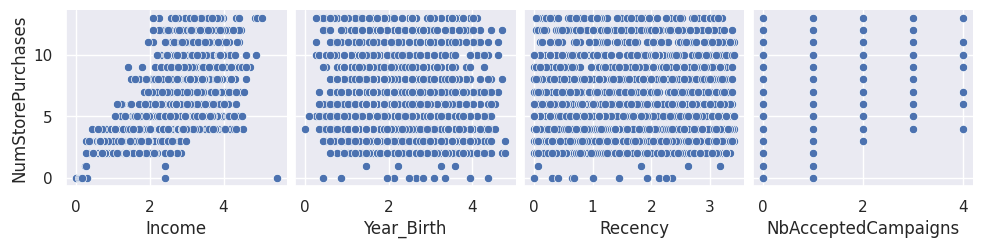
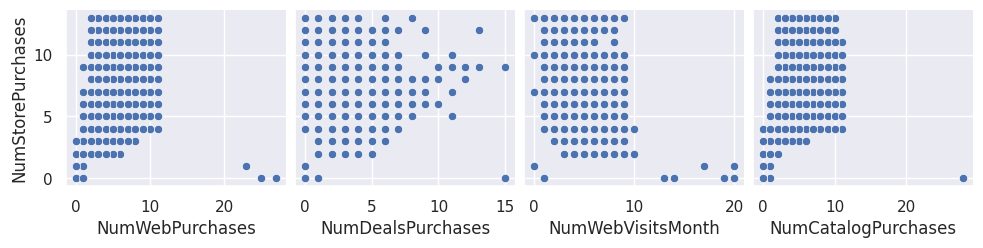
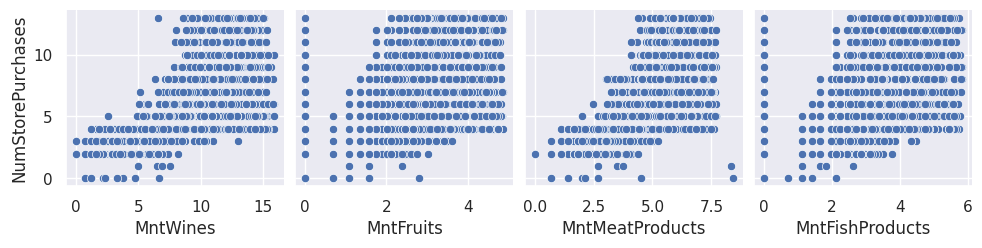
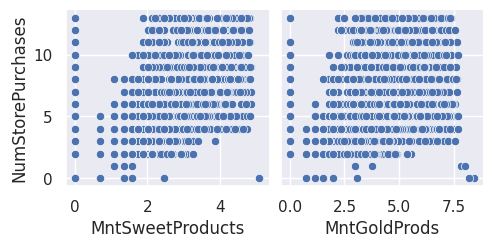
Hypothèse 1 : lien linéaire entre Y et les variables explicatives numériques#
1sns.pairplot(df_transforme, x_vars=var_numeriques_reg[0:4], y_vars="NumStorePurchases")
2sns.pairplot(df_transforme, x_vars=var_numeriques_reg[4:8], y_vars="NumStorePurchases")
3sns.pairplot(df_transforme, x_vars=var_numeriques_reg[8:12], y_vars="NumStorePurchases")
4sns.pairplot(df_transforme, x_vars=var_numeriques_reg[12:], y_vars="NumStorePurchases")
<seaborn.axisgrid.PairGrid at 0x7f94fd9e1f30>
1for x in X[var_numeriques_reg].columns:
2 corr = pearsonr(X[x], Y)
3 print(
4 "Le coefficient de corrélation linéaire entre Y et",
5 x,
6 "vaut",
7 corr[0],
8 "la pvalue vaut",
9 corr[1],
10 )
Le coefficient de corrélation linéaire entre Y et Income vaut 0.6790710752806047 la pvalue vaut 1.3161539637560999e-276
Le coefficient de corrélation linéaire entre Y et Year_Birth vaut -0.14526120372623744 la pvalue vaut 4.1123238450486986e-11
Le coefficient de corrélation linéaire entre Y et Recency vaut 0.001463326219470877 la pvalue vaut 0.9472714287541293
Le coefficient de corrélation linéaire entre Y et NbAcceptedCampaigns vaut 0.21234097582784053 la pvalue vaut 2.8026864212886505e-22
Le coefficient de corrélation linéaire entre Y et NumWebPurchases vaut 0.4868594514010033 la pvalue vaut 3.457837889457746e-122
Le coefficient de corrélation linéaire entre Y et NumDealsPurchases vaut 0.07208375232131894 la pvalue vaut 0.0011062951780020662
Le coefficient de corrélation linéaire entre Y et NumWebVisitsMonth vaut -0.43919311950774226 la pvalue vaut 3.425052472177628e-97
Le coefficient de corrélation linéaire entre Y et NumCatalogPurchases vaut 0.5627033023451984 la pvalue vaut 3.924437146611002e-171
Le coefficient de corrélation linéaire entre Y et MntWines vaut 0.7427337091436748 la pvalue vaut 0.0
Le coefficient de corrélation linéaire entre Y et MntFruits vaut 0.5313945643467054 la pvalue vaut 2.074678857407921e-149
Le coefficient de corrélation linéaire entre Y et MntMeatProducts vaut 0.7101686508975804 la pvalue vaut 1.06156040464e-313
Le coefficient de corrélation linéaire entre Y et MntFishProducts vaut 0.5313511939986364 la pvalue vaut 2.215537485896551e-149
Le coefficient de corrélation linéaire entre Y et MntSweetProducts vaut 0.5374817998598812 la pvalue vaut 1.8679386261982883e-153
Le coefficient de corrélation linéaire entre Y et MntGoldProds vaut 0.46958362271100534 la pvalue vaut 1.1467326528065478e-112
1## TODO: faire un joli affichage avec SNS heatmap
On décide déjà d’écarter la variable Recency de la régression.
1del X["Recency"]
2var_numeriques_reg.remove("Recency")
Réalisation du modèle#
1X_train, X_test, Y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
1model_multiple = LinearRegression().fit(X_train, Y_train)
2Y_train_hat = model_multiple.predict(X_train)
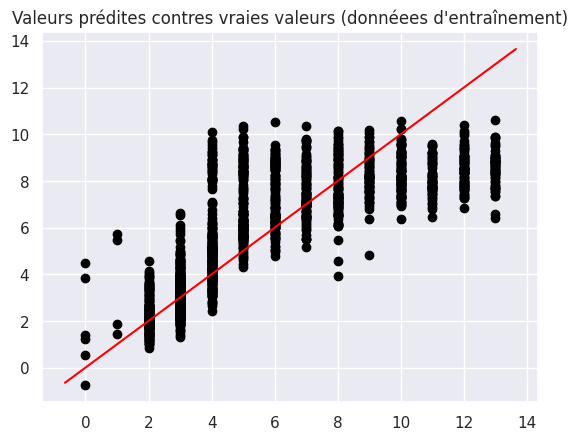
1plt.scatter(Y_train, Y_train_hat, color="black")
2plt.title("Valeurs prédites contres vraies valeurs (donnéees d'entraînement)")
3abline(1, 0)
Hypothèse 2 : exogénéité sur les variables numériques#
(Cela n’a pas de sens de tester l’exogénéité sur les variables catégoriques car la notion de corrélation ne fonctionne pas avec celles-ci.)
1residuals = Y_train - Y_train_hat
1for x in X_train[var_numeriques_reg].columns:
2 corr = pearsonr(X_train[x], residuals)
3 print(
4 "Le coefficient de corrélation entre",
5 x,
6 "et les residus vaut",
7 corr[0],
8 "et la pvalue associée vaut",
9 corr[1],
10 )
Le coefficient de corrélation entre Income et les residus vaut -5.2827750854356204e-17 et la pvalue associée vaut 0.9999999999999989
Le coefficient de corrélation entre Year_Birth et les residus vaut 2.2936296958930846e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre NbAcceptedCampaigns et les residus vaut -1.288574281999022e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre NumWebPurchases et les residus vaut 1.1798830142073502e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre NumDealsPurchases et les residus vaut 1.285592726024687e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre NumWebVisitsMonth et les residus vaut 1.140038584368508e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre NumCatalogPurchases et les residus vaut -1.060078674147702e-16 et la pvalue associée vaut 0.9999999999999989
Le coefficient de corrélation entre MntWines et les residus vaut -4.4289658746032856e-17 et la pvalue associée vaut 0.9999999999999989
Le coefficient de corrélation entre MntFruits et les residus vaut 1.42409955355971e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre MntMeatProducts et les residus vaut 8.355132991716419e-18 et la pvalue associée vaut 0.9999999999999989
Le coefficient de corrélation entre MntFishProducts et les residus vaut 9.23198149871407e-17 et la pvalue associée vaut 0.9999999999999989
Le coefficient de corrélation entre MntSweetProducts et les residus vaut 1.5135462327897642e-16 et la pvalue associée vaut 0.9999999999999919
Le coefficient de corrélation entre MntGoldProds et les residus vaut 7.925517880869037e-17 et la pvalue associée vaut 0.9999999999999989
Il n’y a pas d’endogénéité.
Hypothèse 3 : l’erreur suit une loi normale centrée i.e. $E(ε_i) = 0$#
1plt.hist(residuals, density=True)
2
3x = np.linspace(-6, 6, 100)
4plt.plot(x, stats.norm.pdf(x, 0, 1))
5plt.title("Histogramme des résidus en superposition avec la densité de la loi normale")
6plt.show()
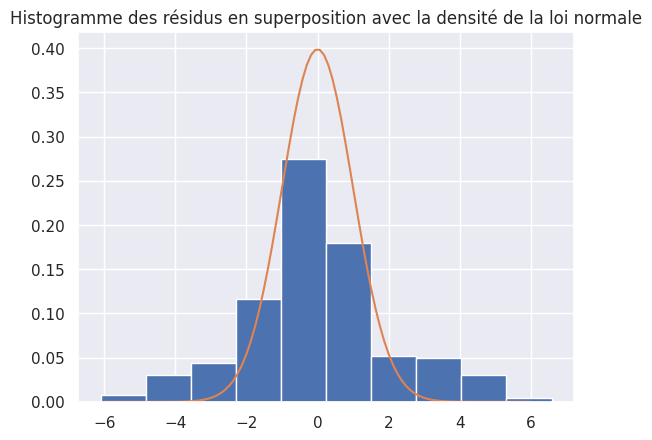
1print("La moyenne des résidus vaut", statistics.mean(residuals))
La moyenne des résidus vaut -4.766629905236613e-16
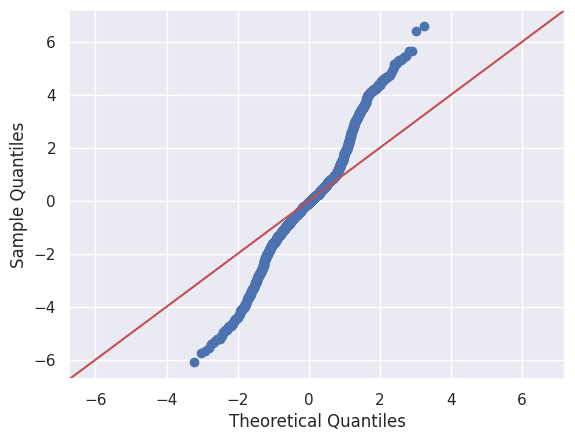
1sm.qqplot(residuals, line="45")
2print("On constate sur le qqplot que les points ne suivent pas la droite x = y")
On constate sur le qqplot que les points ne suivent pas la droite x = y
1print(
2 "Un test de shapiro, pour tester l'hypothèse de normalité, nous donne une pvalue de",
3 stats.shapiro(residuals)[1],
4 ". On rejette l'hypothèse nulle et on conclut que les résidus ne suivent pas une loi normale.",
5)
Un test de shapiro, pour tester l'hypothèse de normalité, nous donne une pvalue de 3.973341823017073e-16 . On rejette l'hypothèse nulle et on conclut que les résidus ne suivent pas une loi normale.
Hypothèse 4 : homoscédasticité#
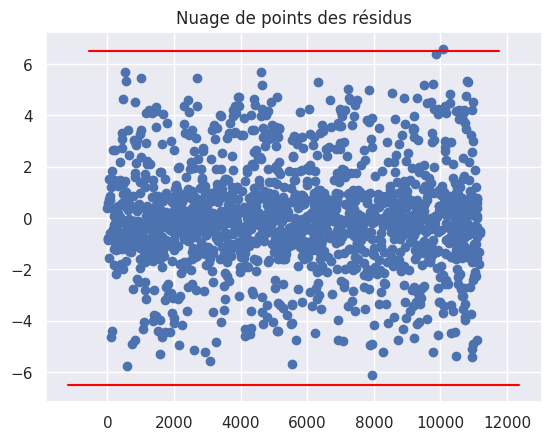
1plt.plot(residuals, "bo")
2plt.title("Nuage de points des résidus")
3abline(0, 6.5)
4abline(0, -6.5)
1fit = sm.OLS(Y_train, sm.add_constant(X_train)).fit()
1fit.summary()
| Dep. Variable: | NumStorePurchases | R-squared: | 0.623 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.617 |
| Method: | Least Squares | F-statistic: | 120.9 |
| Date: | Sun, 17 Dec 2023 | Prob (F-statistic): | 1.60e-321 |
| Time: | 21:40:30 | Log-Likelihood: | -3449.1 |
| No. Observations: | 1636 | AIC: | 6944. |
| Df Residuals: | 1613 | BIC: | 7068. |
| Df Model: | 22 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 1.1164 | 0.263 | 4.252 | 0.000 | 0.601 | 1.632 |
| NbChildren | -0.2059 | 0.099 | -2.087 | 0.037 | -0.399 | -0.012 |
| Education_2n Cycle | 0.4084 | 0.166 | 2.455 | 0.014 | 0.082 | 0.735 |
| Education_Basic | 0.6801 | 0.288 | 2.361 | 0.018 | 0.115 | 1.245 |
| Education_Graduation | 0.0099 | 0.112 | 0.088 | 0.930 | -0.211 | 0.230 |
| Education_Master | -0.0326 | 0.139 | -0.234 | 0.815 | -0.306 | 0.240 |
| Education_PhD | 0.0506 | 0.136 | 0.372 | 0.710 | -0.217 | 0.318 |
| Marital_Status_Divorced | 0.3121 | 0.150 | 2.076 | 0.038 | 0.017 | 0.607 |
| Marital_Status_Married | 0.3234 | 0.104 | 3.103 | 0.002 | 0.119 | 0.528 |
| Marital_Status_Single | 0.0786 | 0.121 | 0.650 | 0.516 | -0.159 | 0.316 |
| Marital_Status_Together | 0.1935 | 0.113 | 1.713 | 0.087 | -0.028 | 0.415 |
| Marital_Status_Widow | 0.2090 | 0.229 | 0.911 | 0.362 | -0.241 | 0.659 |
| Income | 0.2647 | 0.128 | 2.074 | 0.038 | 0.014 | 0.515 |
| Year_Birth | 0.0576 | 0.055 | 1.043 | 0.297 | -0.051 | 0.166 |
| NbAcceptedCampaigns | -0.3867 | 0.084 | -4.617 | 0.000 | -0.551 | -0.222 |
| NumWebPurchases | 0.0437 | 0.028 | 1.561 | 0.119 | -0.011 | 0.099 |
| NumDealsPurchases | 0.1072 | 0.037 | 2.927 | 0.003 | 0.035 | 0.179 |
| NumWebVisitsMonth | -0.1821 | 0.032 | -5.618 | 0.000 | -0.246 | -0.119 |
| NumCatalogPurchases | -0.1065 | 0.029 | -3.639 | 0.000 | -0.164 | -0.049 |
| MntWines | 0.4101 | 0.033 | 12.471 | 0.000 | 0.346 | 0.475 |
| MntFruits | 0.1047 | 0.055 | 1.887 | 0.059 | -0.004 | 0.214 |
| MntMeatProducts | 0.1076 | 0.077 | 1.407 | 0.160 | -0.042 | 0.258 |
| MntFishProducts | 0.1247 | 0.048 | 2.584 | 0.010 | 0.030 | 0.219 |
| MntSweetProducts | 0.2224 | 0.054 | 4.147 | 0.000 | 0.117 | 0.328 |
| MntGoldProds | -0.0399 | 0.039 | -1.034 | 0.302 | -0.116 | 0.036 |
| Omnibus: | 23.189 | Durbin-Watson: | 2.023 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 32.807 |
| Skew: | 0.156 | Prob(JB): | 7.52e-08 |
| Kurtosis: | 3.620 | Cond. No. | 4.03e+16 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 2.16e-28. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
1res_names = ["F statistic", "p-value"]
2gq_test = sms.het_goldfeldquandt(fit.resid, fit.model.exog)
3lzip(res_names, gq_test)
[('F statistic', 1.005758558851296), ('p-value', 0.46775077410560034)]
1bp_test = sms.het_breuschpagan(fit.resid, fit.model.exog)
2lzip(res_names, bp_test)
[('F statistic', 482.3119535871289), ('p-value', 7.7911043046153805e-87)]
1white_test = sms.het_white(fit.resid, fit.model.exog)
2lzip(res_names, white_test)
[('F statistic', 792.4970486154685), ('p-value', 1.1109502140244515e-56)]
Le test de Goldfeld-Quandt, qui vérifie la constance de la variance entre deux échantillons, ne nous donne pas d’hétéroscédasticité, contrairement aux tests de White et de Breusch-Pagan.
Hypothèse 5 : absence d’autocorrélation#
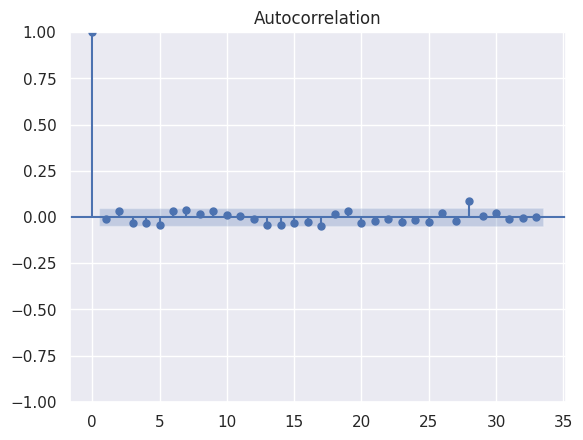
1sm.graphics.tsa.plot_acf(residuals)
2print("On remarque une absence d'autocorrélation.")
On remarque une absence d'autocorrélation.
Hypothèse 6 : absence de multicolinéarité#
Calcul de la matrice $X^t \times X$ et de son déterminant :
1X_train_matrix = X_train.to_numpy()
2X_train_matrix_transpose = np.matrix.transpose(X_train_matrix)
1det = np.linalg.det(np.matmul(X_train_matrix_transpose, X_train_matrix))
2det
-3.175207570697781e+53
Variance Inflation Factor#
$$ VIF_i = 1 / ( 1 − R_i^2 ) $$ où $R_i^2 =$ coefficient de détermination non ajusté pour la régression de la ième variable indépendante sur les autres variables restantes
Le facteur d’inflation de la variance est une mesure de l’augmentation de la variance des estimations de paramètres si une variable supplémentaire est ajoutée à la régression linéaire. C’est une mesure de la multicolinéarité de la matrice des variables explicatives.
Une recommandation est que si le VIF est supérieur à 10, alors la variable explicative en question est fortement colinéaire avec les autres variables explicatives, et les estimations de paramètres auront de grandes erreurs en raison de cela.
Cf la documentation de statsmodels
1vif = [
2 variance_inflation_factor(sm.add_constant(X_train).values, i)
3 for i in range(sm.add_constant(X_train).shape[1])
4]
5## Rq: la fonction VIF attend une constante dans le dataframe d'entree
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/regression/linear_model.py:1752: RuntimeWarning: divide by zero encountered in scalar divide
return 1 - self.ssr/self.centered_tss
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/statsmodels/stats/outliers_influence.py:195: RuntimeWarning: divide by zero encountered in scalar divide
vif = 1. / (1. - r_squared_i)
1print(pd.DataFrame({"VIF": vif[1:]}, index=X_train.columns))
VIF
NbChildren 2.275998
Education_2n Cycle inf
Education_Basic inf
Education_Graduation inf
Education_Master inf
Education_PhD inf
Marital_Status_Divorced inf
Marital_Status_Married inf
Marital_Status_Single inf
Marital_Status_Together inf
Marital_Status_Widow inf
Income 6.679390
Year_Birth 1.224293
NbAcceptedCampaigns 1.356774
NumWebPurchases 2.358240
NumDealsPurchases 1.961293
NumWebVisitsMonth 2.516005
NumCatalogPurchases 2.813537
MntWines 7.709258
MntFruits 2.670042
MntMeatProducts 7.505137
MntFishProducts 2.832624
MntSweetProducts 2.586210
MntGoldProds 1.995179
Réduction du nombre de variables explicatives par le critère AIC#
Le critère d’information d’Akaike s’écrit comme suit :
$$ AIC = 2 \times k - 2 \times \ln(L) $$
où k est le nombre de paramètres à estimer du modèle et L est le maximum de la fonction de vraisemblance du modèle.
1def aic(X, Y, regressor=""): ## entrer X le dataframe des variables explicatives,
2 ## Y la variable expliquée, et le regresseur utilisé
3 aic_list = []
4
5 for col in X.columns:
6 X_temp = X.drop(col, axis=1)
7
8 if regressor == "linearOLS":
9 model_temp = sm.OLS(Y, sm.add_constant(X_temp)).fit()
10 elif regressor == "GLMpoisson":
11 model_temp = sm.GLM(
12 Y, sm.add_constant(X_temp), family=sm.families.Poisson()
13 ).fit()
14
15 else:
16 return "Entrer un régresseur valide"
17
18 aic_list.append([col, model_temp.aic])
19
20 return aic_list
1def stepwise(X, Y, regressor=""): ## entrer X le dataframe des variables explicatives,
2 ## Y la variable expliquée, et le regresseur utilisé
3
4 if regressor == "linearOLS":
5 current_aic = (
6 sm.OLS(Y, sm.add_constant(X)).fit().aic
7 ) ## aic avec les variables actuelles
8 elif regressor == "GLMpoisson":
9 current_aic = (
10 sm.GLM(Y, sm.add_constant(X), family=sm.families.Poisson()).fit().aic
11 )
12 else:
13 return "Entrer un régresseur valide"
14
15 aic_list = aic(
16 X, Y, regressor
17 ) ## liste des aic par supression des variables une a une
18
19 my_bool = 0 ## pour indiquer si aucune variable n'est a enlever
20 for i in range(
21 len(aic_list)
22 ): ## si l'aic diminue pour une variable supprimee, on enleve cette variable du df X
23
24 if aic_list[i][1] < current_aic:
25 del X[aic_list[i][0]] ## a l'interieur des crochets c'est une string
26 my_bool = 1
27
28 if my_bool == 0:
29 return "L'algorithme stepwise est terminé."
1print("Avant l'AIC, le nombre de variables explicatives est :", X_train.shape[1])
Avant l'AIC, le nombre de variables explicatives est : 24
1while True:
2 if (
3 stepwise(X_train, Y_train, regressor="linearOLS")
4 == "L'algorithme stepwise est terminé."
5 ):
6 break
1stepwise(X_train, Y_train, regressor="linearOLS")
"L'algorithme stepwise est terminé."
1print("Après l'AIC, le nombre de variables explicatives est :", X_train.shape[1])
Après l'AIC, le nombre de variables explicatives est : 14
1## on refait les modèles après sélection de variables
2
3X_test = X_test[
4 X_train.columns
5] ## homogénéisation des données de test et d'entraînement
6
7fit = sm.OLS(Y_train, sm.add_constant(X_train)).fit()
8
9model_multiple = LinearRegression().fit(X_train, Y_train)
Distance de Cook#
1influence = fit.get_influence()
2cooks = influence.cooks_distance
1plt.scatter(X_train.index, cooks[0])
2plt.xlabel("Index des individus")
3plt.ylabel("Distances de Cook")
4plt.show()
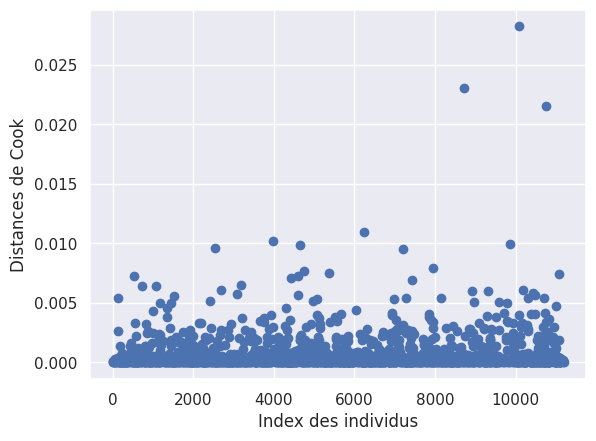
1cooks_indexes = [i for i, x in enumerate(cooks[0] > 0.010) if x]
2## détermine l'index dans la liste des individus dont la distance de cook dépasse 0.010
1extreme_ind_list = [X_train.iloc[[i]].index[0] for i in cooks_indexes]
2
3for ind in extreme_ind_list:
4 print(ind)
10749
6237
3968
8720
10089
1## TODO: supprimer les individus aux distances trop grandes
1influence_plot(fit)
2print("")
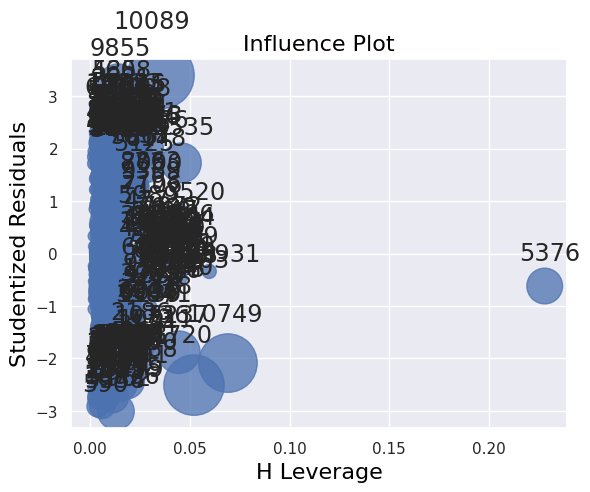
1X_train.drop(extreme_ind_list + [5316], inplace=True)
2Y_train.drop(extreme_ind_list + [5316], inplace=True)
1## on refait les modèles après suppression des individus extremes
2
3X_test = X_test[
4 X_train.columns
5] ## homogénéisation des données de test et d'entraînement
6
7fit = sm.OLS(Y_train, sm.add_constant(X_train)).fit()
8
9model_multiple = LinearRegression().fit(X_train, Y_train)
Les distances de Cook ont été largement réduites par la sélection de variables au critère AIC.
Score du modèle#
Qualité d’ajustement#
1print(f"Le R² du modèle vaut {model_multiple.score(X_train, Y_train)}")
Le R² du modèle vaut 0.62475575488369
1Y_train_hat = model_multiple.predict(X_train)
1mse_train_lineaire_multiple = mean_squared_error(Y_train, Y_train_hat)
2rmse_train_lineaire_multiple = mean_squared_error(Y_train, Y_train_hat, squared=False)
3mae_train_lineaire_multiple = mean_absolute_error(Y_train, Y_train_hat)
1print(f"MSE = {mse_train_lineaire_multiple}")
2print(f"RMSE = {rmse_train_lineaire_multiple}")
3print(f"MAE = {mae_train_lineaire_multiple}")
MSE = 3.9212570253960792
RMSE = 1.9802164087281167
MAE = 1.4484641568191754
1print(f"MSE = {mean_squared_error(Y_train, Y_train_hat)}")
2print(f"RMSE = {mean_squared_error(Y_train, Y_train_hat, squared=False)}")
3print(f"MAE = {mean_absolute_error(Y_train, Y_train_hat)}")
MSE = 3.9212570253960792
RMSE = 1.9802164087281167
MAE = 1.4484641568191754
Qualité de prédiction#
Train / test split
1print(
2 f"R² du modèle sur les données d'entraînement = {model_multiple.score(X_train, Y_train)}"
3)
4print(f"R² du modèle sur les données de test = {model_multiple.score(X_test, y_test)}")
R² du modèle sur les données d'entraînement = 0.62475575488369
R² du modèle sur les données de test = 0.6129578160565867
1y_pred = model_multiple.predict(X_test)
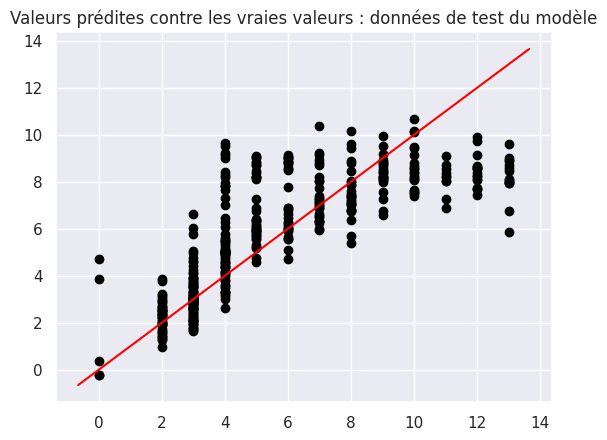
1plt.scatter(y_test, y_pred, color="black")
2abline(1, 0)
3plt.title("Valeurs prédites contre les vraies valeurs : données de test du modèle")
Text(0.5, 1.0, 'Valeurs prédites contre les vraies valeurs : données de test du modèle')
1affiche_score(model, y_test, y_pred)
MSE = 3.923373743247052
RMSE = 1.9807508029146554
MAE = 1.4130411421162983
1nom_modele = "Régression multiple"
2ajout_score(model, nom_modele, y_test, y_pred)
Régression par modèle linéaire généralisé (GLM) : régression de Poisson#
Notons $Y$ notre variable d’intérêt et $X_1, …, X_P$ nos variables explicatives.
On suppose que Y suit une loi de Poisson de paramètre $\lambda \in \mathbb{R+*}$
On cherche à déterminer les coefficients de l’équation :
$\log(\mathrm{E}(Y|X)) = \log( \lambda ) = \alpha + \beta_1 X_1 + \beta_2 X_2 + … + \beta_P X_P $
Ce qui revient à déterminer les coefficients de l’équation :
$\lambda = e^{\alpha + \beta_1 X_1 + \beta_2 X_2 + … + \beta_P X_P}$
L’objectif de la régression est d’estimer $\alpha, \beta_1, …, \beta_P$. Une fois ces coefficients estimés, on peut déterminer, pour un nouveau vecteur $X$, $E(Y|X) = e^{\alpha + \beta_1 X_1 + \beta_2 X_2 + … + \beta_P X_P}$
Hypothèses à vérifier :#
- Avant de choisir la régression de Poisson :
La variable d’intérêt doit être une variable de comptage, à valeurs entières positives.
La variable d’intérêt doit suivre une loi de Poisson :
$Y | X ∼ Poisson(\lambda)$, où $\lambda \in \mathbb{R+*}$ , en particulier, la moyenne de Y doit être égale à sa variance.$log(\lambda)$ est une fonction linéaire de $X_1, X_2, … , X_P$
- A posteriori :
$Cov(X_i, ε_j) = 0$, pour tout $i, j \in N \times N, i \neq j$ (exogénéité) et pour chaque variable explicative $X_p$
L’erreur suit une loi normale centrée i.e. $E(ε_i) = 0$
L’erreur est de variance constante (homoscédasticité) i.e $Var(ε_i) = \sigma^2$, une constante
Les erreurs sont indépendantes (absence d’autocorrélation) i.e. $Cov(εi, εj) = 0$, pour tout $i, j \in N \times N, i \neq j$
Absence de colinéarité entre les variables explicatives, i.e. $X^t * X$ est régulière, $det(X^t * X) \neq 0$
1X = df_reg[var_categoriques_reg + var_numeriques_reg]
2Y = df["NumStorePurchases"]
Hypothèses 1 : nature de la variable d’intérêt#
La variable NumberStorePurchases désigne le nombre d’achat effectués en magasin. C’est bien une variable de comptage dont les valeurs sont entières et positives.
Hypothèse 2 : loi de Poisson ?#
1plt.hist(df["NumStorePurchases"], density=True)
2
3## creating a numpy array for x-axis
4x = np.arange(0, 20, 1)
5
6## poisson distribution data for y-axis
7y = poisson.pmf(x, mu=5)
8
9plt.plot(x, y)
10plt.plot()
[]
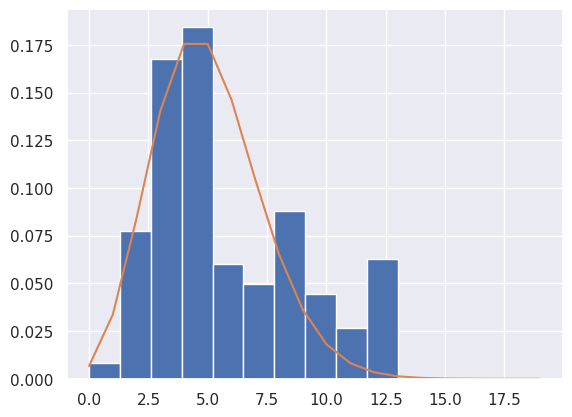
1ks_statistic, p_value = kstest(df["NumStorePurchases"], "poisson", args=(5, 0))
2print(ks_statistic, p_value)
0.22040539061928222 5.04003553934594e-88
1print(
2 "Variance de Y :",
3 df["NumStorePurchases"].var(),
4 ": Espérance de Y:",
5 df["NumStorePurchases"].mean(),
6)
Variance de Y : 10.511054846064726 : Espérance de Y: 5.772904483430799
1print(
2 "La variance et l'espérance de Y ne sont pas égales. Cela peut dégrader la qualité de notre régression."
3)
La variance et l'espérance de Y ne sont pas égales. Cela peut dégrader la qualité de notre régression.
Hypothèse 3 : lien linéaire entre $log(Y)$ et $X_1, …, X_P$#
1null_index = Y[Y == 0].index
2## on élimine les 0 pour appliquer le log
1sns.pairplot(
2 pd.concat(
3 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
4 axis=1,
5 ),
6 x_vars=var_numeriques_reg[0:4],
7 y_vars="NumStorePurchases",
8)
9sns.pairplot(
10 pd.concat(
11 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
12 axis=1,
13 ),
14 x_vars=var_numeriques_reg[4:8],
15 y_vars="NumStorePurchases",
16)
17sns.pairplot(
18 pd.concat(
19 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
20 axis=1,
21 ),
22 x_vars=var_numeriques_reg[8:12],
23 y_vars="NumStorePurchases",
24)
25sns.pairplot(
26 pd.concat(
27 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
28 axis=1,
29 ),
30 x_vars=var_numeriques_reg[12:],
31 y_vars="NumStorePurchases",
32)
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
Cell In[100], line 3
1 sns.pairplot(
2 pd.concat(
----> 3 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
4 axis=1,
5 ),
6 x_vars=var_numeriques_reg[0:4],
7 y_vars="NumStorePurchases",
8 )
9 sns.pairplot(
10 pd.concat(
11 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
(...)
15 y_vars="NumStorePurchases",
16 )
17 sns.pairplot(
18 pd.concat(
19 [X.drop(index=null_index, axis=0), np.log(Y.drop(index=null_index, axis=0))],
(...)
23 y_vars="NumStorePurchases",
24 )
File ~/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/pandas/util/_decorators.py:331, in deprecate_nonkeyword_arguments.<locals>.decorate.<locals>.wrapper(*args, **kwargs)
325 if len(args) > num_allow_args:
326 warnings.warn(
327 msg.format(arguments=_format_argument_list(allow_args)),
328 FutureWarning,
329 stacklevel=find_stack_level(),
330 )
--> 331 return func(*args, **kwargs)
File ~/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/pandas/core/frame.py:5399, in DataFrame.drop(self, labels, axis, index, columns, level, inplace, errors)
5251 @deprecate_nonkeyword_arguments(version=None, allowed_args=["self", "labels"])
5252 def drop( # type: ignore[override]
5253 self,
(...)
5260 errors: IgnoreRaise = "raise",
5261 ) -> DataFrame | None:
5262 """
5263 Drop specified labels from rows or columns.
5264
(...)
5397 weight 1.0 0.8
5398 """
-> 5399 return super().drop(
5400 labels=labels,
5401 axis=axis,
5402 index=index,
5403 columns=columns,
5404 level=level,
5405 inplace=inplace,
5406 errors=errors,
5407 )
File ~/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/pandas/util/_decorators.py:331, in deprecate_nonkeyword_arguments.<locals>.decorate.<locals>.wrapper(*args, **kwargs)
325 if len(args) > num_allow_args:
326 warnings.warn(
327 msg.format(arguments=_format_argument_list(allow_args)),
328 FutureWarning,
329 stacklevel=find_stack_level(),
330 )
--> 331 return func(*args, **kwargs)
File ~/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/pandas/core/generic.py:4505, in NDFrame.drop(self, labels, axis, index, columns, level, inplace, errors)
4503 for axis, labels in axes.items():
4504 if labels is not None:
-> 4505 obj = obj._drop_axis(labels, axis, level=level, errors=errors)
4507 if inplace:
4508 self._update_inplace(obj)
File ~/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/pandas/core/generic.py:4546, in NDFrame._drop_axis(self, labels, axis, level, errors, only_slice)
4544 new_axis = axis.drop(labels, level=level, errors=errors)
4545 else:
-> 4546 new_axis = axis.drop(labels, errors=errors)
4547 indexer = axis.get_indexer(new_axis)
4549 # Case for non-unique axis
4550 else:
File ~/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/pandas/core/indexes/base.py:6934, in Index.drop(self, labels, errors)
6932 if mask.any():
6933 if errors != "ignore":
-> 6934 raise KeyError(f"{list(labels[mask])} not found in axis")
6935 indexer = indexer[~mask]
6936 return self.delete(indexer)
KeyError: '[8475, 5555, 4931, 11181] not found in axis'
1for x in X[var_numeriques_reg].columns:
2 corr = pearsonr(
3 X.drop(index=null_index, axis=0)[x], np.log(Y.drop(index=null_index, axis=0))
4 )
5 print(
6 "Le coefficient de corrélation linéaire entre log(Y) et",
7 x,
8 "vaut",
9 corr[0],
10 "la pvalue vaut",
11 corr[1],
12 )
Il existe bien un lien linéaire entre $log(Y)$ et les variables explicatives.
Réalisation du modèle#
1X_train, X_test, Y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
1model_poisson = PoissonRegressor().fit(X_train, Y_train)
2Y_train_hat = model_poisson.predict(X_train)
Ici, notre fonction de lien est $f(\lambda) = log(\lambda)$
Elle est utilisée par défaut par sci-kit learn
1plt.scatter(Y_train, Y_train_hat, color="black")
2plt.title("Valeurs prédites contres vraies valeurs (donnéees d'entraînement)")
3abline(1, 0)
Hypothèse 4 : exogénéité sur les variables numériques#
(Cela n’a pas de sens de tester l’exogénéité sur les variables catégoriques car la notion de corrélation ne fonctionne pas avec celles-ci.)
1residuals = Y_train - Y_train_hat
1for x in X_train[var_numeriques_reg].columns:
2 corr = pearsonr(X_train[x], residuals)
3 print(
4 "Le coefficient de corrélation entre",
5 x,
6 "et les residus vaut",
7 corr[0],
8 "et la pvalue associée vaut",
9 corr[1],
10 )
Il n’y a pas d’endogénéité.
Hypothèse 5 : l’erreur suit une loi normale centrée i.e. $E(ε_i) = 0$#
1plt.hist(residuals, density=True)
2
3x = np.linspace(-6, 6, 100)
4plt.plot(x, stats.norm.pdf(x, 0, 1))
5plt.title("Histogramme des résidus en superposition avec la densité de la loi normale")
6plt.show()
1print("La moyenne des résidus vaut", statistics.mean(residuals))
1sm.qqplot(residuals, line="45")
2print("On constate sur le qqplot que les points ne suivent pas la droite x = y")
1print(
2 "Un test de shapiro, pour tester l'hypothèse de normalité, nous donne une pvalue de",
3 stats.shapiro(residuals)[1],
4 ". On rejette l'hypothèse nulle et on conclut que les résidus ne suivent pas une loi normale.",
5)
Hypothèse 6 : homoscédasticité#
1plt.plot(residuals, "bo")
2plt.title("Nuage de points des résidus")
3abline(0, 6.5)
4abline(0, -6.5)
1fit = sm.GLM(Y_train, sm.add_constant(X_train), family=sm.families.Poisson()).fit()
1fit.summary()
1res_names = ["F statistic", "p-value"]
2gq_test = sms.het_goldfeldquandt(fit.resid_response, fit.model.exog)
3lzip(res_names, gq_test)
La pvalue du test de Goldfeld-Quandt est supérieure à 0.05 dont on conserve l’hypothèse d’homoscédasticité au seuil de 5% (et même au delà).
Hypothèse 7 : absence d’autocorrélation#
1sm.graphics.tsa.plot_acf(residuals)
2print("On remarque une absence d'autocorrélation.")
Hypothèse 8 : absence de multicolinéarité#
1vif = [
2 variance_inflation_factor(sm.add_constant(X_train).values, i)
3 for i in range(sm.add_constant(X_train).shape[1])
4]
5## Rq: la fonction VIF attend une constante dans le dataframe d'entree
1print(pd.DataFrame({"VIF": vif[1:]}, index=X_train.columns))
Réduction du nombre de variables explicatives par le critère AIC#
1print("Avant l'AIC, le nombre de variables explicatives est :", X_train.shape[1])
1while True:
2 if (
3 stepwise(X_train, Y_train, regressor="GLMpoisson")
4 == "L'algorithme stepwise est terminé."
5 ):
6 break
1stepwise(X_train, Y_train, regressor="GLMpoisson")
1print("Après l'AIC, le nombre de variables explicatives est :", X_train.shape[1])
1## on refait les modèles après sélection de variables
2
3X_test = X_test[
4 X_train.columns
5] ## homogénéisation des données de test et d'entraînement
6
7fit = sm.GLM(Y_train, sm.add_constant(X_train), family=sm.families.Poisson()).fit()
8
9model_poisson = PoissonRegressor().fit(X_train, Y_train)
Distance de Cook#
1influence = fit.get_influence()
2cooks = influence.cooks_distance
1plt.scatter(X_train.index, cooks[0])
2plt.xlabel("Index des individus")
3plt.ylabel("Distances de Cook")
4plt.show()
1cooks_indexes = [i for i, x in enumerate(cooks[0] > 0.010) if x]
2## détermine l'index dans la liste des individus dont la distance de cook dépasse 0.010
1extreme_ind_list = [X_train.iloc[[i]].index[0] for i in cooks_indexes]
2
3for ind in extreme_ind_list:
4 print(ind)
1X_train.drop(extreme_ind_list, inplace=True)
2Y_train.drop(extreme_ind_list, inplace=True)
1## on refait les modèles après suppression des individus extremes
2
3X_test = X_test[
4 X_train.columns
5] ## homogénéisation des données de test et d'entraînement
6
7fit = sm.GLM(Y_train, sm.add_constant(X_train), family=sm.families.Poisson()).fit()
8
9model_poisson = PoissonRegressor().fit(X_train, Y_train)
1## Remarque : statsmodels ne fait pas d'influence plot pour les modeles GLM
Score du modèle#
Qualité d’ajustement#
1print(f"Le R² du modèle vaut {model_poisson.score(X_train, Y_train)}")
1Y_train_hat = model_poisson.predict(X_train)
1mse_train_poisson = mean_squared_error(Y_train, Y_train_hat)
2rmse_train_poisson = mean_squared_error(Y_train, Y_train_hat, squared=False)
3mae_train_poisson = mean_absolute_error(Y_train, Y_train_hat)
1print(f"MSE = {mse_train_poisson}")
2print(f"RMSE = {rmse_train_poisson}")
3print(f"MAE = {mae_train_poisson}")
Qualité de prédiction#
Train / test split
1print(
2 f"R² du modèle sur les données d'entraînement = {model_poisson.score(X_train, Y_train)}"
3)
4print(f"R² du modèle sur les données de test = {model_poisson.score(X_test, y_test)}")
1y_pred = model_poisson.predict(X_test)
1plt.scatter(y_test, y_pred, color="black")
2abline(1, 0)
3plt.title("Valeurs prédites contre les vraies valeurs : données de test du modèle")
1affiche_score(model, y_test, y_pred)
1nom_modele = "GLM Poisson"
2ajout_score(model, nom_modele, y_test, y_pred)
1print("Constante : ", model_poisson.intercept_)
2for i in range(len(model_poisson.coef_)):
3 print(f" beta_{i + 1} = {model_poisson.coef_[i]} ")
Régression polynomiale#
Création des données#
On conserve les mêmes variables explicatives et la même variable d’intérêt, mais en séparant les variables catégoriques des variables numériques qu’on transformera en monômes.
Ceci car cela n’aurait pas de sens d’élever des variables catégoriques au carré et afin d’éviter l’explosion combinatoire.
1X_ref = df_reg[var_numeriques_reg + var_categoriques_reg]
1X_numeriques = df_reg[var_numeriques_reg]
2X_categoriques = df_reg[var_categoriques_reg]
3Y = df_reg["NumStorePurchases"]
1## Transformer les données en matrice de caractéristiques polynomiales
2poly = PolynomialFeatures(degree=2)
3
4X_poly = poly.fit_transform(X_numeriques)
5## Remarque : pendant la transformation, l'ordre des lignes est conservé, ce qui permettra de remettre les index
1## trouvé sur stack over flow :
2## permet de créer un df à partir de l'objet numpy array en sortie de la fonction fit_transform de sklearn
3
4target_feature_names = [
5 "x".join(["{}^{}".format(pair[0], pair[1]) for pair in tuple if pair[1] != 0])
6 for tuple in [zip(X.columns, p) for p in poly.powers_]
7]
8## détermine les noms de colonnes
9
10
11X_poly = pd.DataFrame(X_poly, columns=target_feature_names)
1## je remets les indexes au df X_poly afin de pouvoir le concaténer avec le df des var categoriques avant la régression
2X_poly = X_poly.set_index(pd.Index(X_categoriques.index))
1X = pd.concat([X_poly, X_categoriques], axis=1)
1X.shape
Bien évidemment, il y a de la redondance dans les variables explicatives et donc de la colinéarité structurelle.
Réalisation du modèle#
1X_train, X_test, Y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
1model_poly = LinearRegression().fit(X_train, Y_train)
2Y_train_hat = model_poly.predict(X_train)
1plt.scatter(Y_train, Y_train_hat, color="black")
2plt.title("Valeurs prédites contres vraies valeurs (donnéees d'entraînement)")
3abline(1, 0)
Réduction du nombre de variables explicatives par le critère AIC#
1print("Avant l'AIC, le nombre de variables explicatives est :", X_train.shape[1])
1while True:
2 if (
3 stepwise(
4 X_train, list(Y_train), regressor="linearOLS"
5 ) ## il faut transformer Y en liste sinon cela bug, je ne sais pas pourquoi
6 == "L'algorithme stepwise est terminé."
7 ):
8 break
1stepwise(X_train, list(Y_train), regressor="linearOLS")
1print("Après l'AIC, le nombre de variables explicatives est :", X_train.shape[1])
La procédure AIC a permi de purifier notre modèle de 77 variables explicatives.
1## on refait les modèles après sélection de variables
2
3X_test = X_test[
4 X_train.columns
5] ## homogénéisation des données de test et d'entraînement
6
7fit = sm.OLS(
8 list(Y_train), sm.add_constant(X_train)
9).fit() ## comme il existe deja une constante dans X_train, statsmodels n'en rajoute pas une deuxieme
10
11model_poly = LinearRegression().fit(X_train, Y_train)
Distance de Cook#
1influence = fit.get_influence()
2cooks = influence.cooks_distance
1plt.scatter(X_train.index, cooks[0])
2plt.xlabel("Index des individus")
3plt.ylabel("Distances de Cook")
4plt.show()
1cooks_indexes = [i for i, x in enumerate(cooks[0] > 0.02) if x]
2## détermine l'index dans la liste des individus dont la distance de cook dépasse 0.010
1extreme_ind_list = [X_train.iloc[[i]].index[0] for i in cooks_indexes]
2
3for ind in extreme_ind_list:
4 print(ind)
1influence_plot(fit)
2print("")
1X_train.drop(extreme_ind_list + [6237, 9058], inplace=True)
2Y_train.drop(extreme_ind_list + [6237, 9058], inplace=True)
1## on refait les modèles après suppression des individus extremes
2
3X_test = X_test[
4 X_train.columns
5] ## homogénéisation des données de test et d'entraînement
6
7fit = sm.OLS(
8 list(Y_train), sm.add_constant(X_train)
9).fit() ## comme il existe deja une constante dans X_train, statsmodels n'en rajoute pas une deuxieme
10
11model_poly = LinearRegression().fit(X_train, Y_train)
1influence = fit.get_influence()
2cooks = influence.cooks_distance
1plt.scatter(X_train.index, cooks[0])
2plt.xlabel("Index des individus")
3plt.ylabel("Distances de Cook")
4plt.show()
1influence_plot(fit)
2print("")
Score du modèle#
Qualité d’ajustement#
1print(f"Le R² du modèle vaut {model_poly.score(X_train, Y_train)}")
1Y_train_hat = model_poly.predict(X_train)
1mse_train_poly = mean_squared_error(Y_train, Y_train_hat)
2rmse_train_poly = mean_squared_error(Y_train, Y_train_hat, squared=False)
3mae_train_poly = mean_absolute_error(Y_train, Y_train_hat)
1print(f"MSE = {mse_train_poly}")
2print(f"RMSE = {rmse_train_poly}")
3print(f"MAE = {mae_train_poly}")
Qualité de prédiction#
Train / test split
1print(
2 f"R² du modèle sur les données d'entraînement = {model_poly.score(X_train, Y_train)}"
3)
4print(f"R² du modèle sur les données de test = {model_poly.score(X_test, y_test)}")
1y_pred = model_poly.predict(X_test)
1plt.scatter(y_test, y_pred, color="black")
2abline(1, 0)
3plt.title("Valeurs prédites contre les vraies valeurs : données de test du modèle")
1print(f"MSE = {mean_squared_error(y_test, y_pred)}")
2print(f"RMSE = {mean_squared_error(y_test, y_pred, squared=False)}")
3print(f"MAE = {mean_absolute_error(y_test, y_pred)}")
La mesure de la qualité d’ajustement à nos données de test est biaisée par des valeurs prédites extrêmes.
1sns.histplot(y_pred)
1y_pred_new = y_pred[y_pred > 0]
2y_test_new = y_test[y_pred > 0]
1plt.scatter(y_test_new, y_pred_new, color="black")
2abline(1, 0)
3plt.title("Valeurs prédites contre les vraies valeurs : données de test du modèle")
1affiche_score(model, y_test, y_pred)
1nom_modele = "Régression polynomiale"
2ajout_score(model, nom_modele, y_test, y_pred)
Corrigé de ces erreurs, le modèle polynomial est notre meilleur modèle.
1print("Constante : ", model_poly.intercept_)
2for i in range(len(model_poly.coef_)):
3 print(f" beta_{i + 1} = {model_poly.coef_[i]} ")
Régression PLS#
Comme nous avons de la multi-colinéarité dans notre modèle, nous allons essayer une méthode de régression robuste face à ce phénomène : la régression PLS.
1X = pd.get_dummies(df_transforme[var_numeriques].drop(columns=["NumStorePurchases"]))
1y = df[["NumStorePurchases"]].astype(int)
1X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
1liste_mae_pls = []
2for n in range(1, 14):
3 pls = PLSRegression(n_components=n)
4
5 pls.fit(X_train, y_train)
6 pls.score(X_train, y_train)
7 y_pred = pls.predict(X_test)
8
9 liste_mae_pls.append(mean_absolute_error(y_test, y_pred))
1plt.title("MAE en fonction du nombre de composantes PLS")
2plt.plot(range(1, 14), liste_mae_pls)
3plt.scatter(np.argmin(liste_mae_pls) + 1, np.min(liste_mae_pls), label="minimum")
4plt.legend()
1print(np.argmin(liste_mae_pls) + 1)
1pls = PLSRegression(n_components=8)
1pls.fit(X_train, y_train)
1pls.score(X_train, y_train)
1y_pred = pls.predict(X_test)
1affiche_score(model, y_test, y_pred)
1nom_modele = "Régression PLS"
2ajout_score(model, nom_modele, y_test, y_pred)
XGBoost#
1X = pd.get_dummies(df_transforme.drop(columns=["NumStorePurchases", "Dt_Customer"]))
1y = df[["NumStorePurchases"]].astype(int)
1X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
1tuned_xgb = xgboost.XGBRegressor(
2 n_estimators=1000,
3 learning_rate=0.05,
4 n_jobs=4,
5 eval_metric="mae",
6 early_stopping_rounds=20,
7 random_state=0,
8)
1tuned_xgb.fit(X_train, y_train, eval_set=[(X_test, y_test)], verbose=False)
1y_pred = tuned_xgb.predict(X_test)
1affiche_score(model, y_test, y_pred)
1nom_modele = "XGBoost"
2ajout_score(model, nom_modele, y_test, y_pred)
Réseau de neurones#
1X_train = np.asarray(X_train).astype("float32")
2y_train = np.asarray(y_train).astype("float32")
3X_test = np.asarray(X_test).astype("float32")
4y_test = np.asarray(y_test).astype("float32")
1X_train.shape
1model = keras.Sequential(
2 [
3 layers.Dense(4, activation="relu", input_shape=[35]),
4 layers.Dense(4, activation="relu"),
5 layers.Dense(1, activation="sigmoid"),
6 ]
7)
1model.compile(
2 optimizer="adam",
3 loss="mean_absolute_error",
4)
1early_stopping = keras.callbacks.EarlyStopping(
2 patience=10,
3 min_delta=0.001,
4 restore_best_weights=True,
5)
1history = model.fit(
2 X_train,
3 y_train,
4 ## validation_data=(X_test, y_test),
5 validation_split=0.2,
6 batch_size=512,
7 epochs=1000,
8 callbacks=[early_stopping],
9 verbose=0, ## hide the output because we have so many epochs
10)
1history_df = pd.DataFrame(history.history)
2## Start the plot at epoch 5
3history_df.loc[5:, ["loss", "val_loss"]].plot()
1y_pred = model.predict(X_test)
1affiche_score(model, y_test, y_pred)
1nom_modele = "Réseau de Neurones"
2ajout_score(model, nom_modele, y_test, y_pred)
Sauvegarde des données#
1score_modeles_df = pd.DataFrame(score_modeles, columns=["Modèle", "Métrique", "Valeur"])
1score_modeles_df.to_csv(f"{data_folder}/results/regressions.csv", index=False)