Analyse factorielle

Import des outils / jeu de données

import matplotlib.pyplot as plt
import pandas as pd
import prince
import seaborn as sns
from mlxtend.plotting import plot_pca_correlation_graph
from sklearn.compose import ColumnTransformer
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

from src.config import data_folder, seed
from src.constants import var_categoriques, var_numeriques
from src.utils import init_notebook

init_notebook()

df = pd.read_csv(
    f"{data_folder}/data-cleaned-feature-engineering.csv",
    sep=",",
    index_col="ID",
    parse_dates=True,
)

Variables globales

var_categoriques_extra = ["NbAcceptedCampaigns", "HasAcceptedCampaigns", "NbChildren"]

var_categoriques_fe = var_categoriques + var_categoriques_extra

Analyse multi-variée

Analyse en Composantes Principales (ACP)

preprocessor = ColumnTransformer(
    transformers=[
        ("scaler", StandardScaler(), var_numeriques),
    ],
)

df_centre_reduit = pd.DataFrame(
    preprocessor.fit_transform(df), columns=df[var_numeriques].columns
)

acp = PCA(random_state=seed)

acp.fit(df_centre_reduit)

PCA(random_state=0)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

variance_expliquee = pd.Series(acp.explained_variance_ratio_)

variance_expliquee

0     0.412215
1     0.112204
2     0.078024
3     0.071339
4     0.057670
5     0.048930
6     0.044279
7     0.037022
8     0.033142
9     0.028891
10    0.025957
11    0.018987
12    0.018062
13    0.013277
dtype: float64

variance_expliquee.plot.barh()

<Axes: >

composantes_principales = pd.DataFrame(
    acp.fit_transform(df_centre_reduit),
    index=df.index,
)

composantes_principales.columns = [
    f"ACP{i+1}" for i in range(composantes_principales.shape[1])
]

composantes_principales.head()

	ACP1	ACP2	ACP3	ACP4	ACP5	ACP6	ACP7	ACP8	ACP9	ACP10	ACP11	ACP12	ACP13	ACP14
ID
5524	3.677574	0.709630	0.726633	0.528046	-1.182996	1.306460	0.193055	2.504792	-0.047630	0.556204	0.381602	-0.026330	-0.831932	-0.118034
2174	-2.024213	-0.621400	-1.365232	-0.600591	-0.685700	0.573463	0.329938	0.081125	0.179518	-0.151067	0.019145	-0.320555	0.072530	0.096130
4141	1.746875	0.152159	-0.131371	-0.971172	-0.509112	-0.986865	-0.950470	-0.534338	-0.504519	0.580976	1.127926	-0.019197	-0.006230	0.247519
6182	-2.384421	-0.746451	0.977139	-0.616917	0.506919	-0.077598	-0.192994	-0.336974	-0.035834	0.130339	0.049029	0.148129	-0.085955	-0.295272
5324	-0.000948	0.499014	0.578226	1.686209	0.749782	0.831949	-0.595007	-0.619262	0.027489	-0.355356	0.727407	-0.405869	-0.187491	0.173714

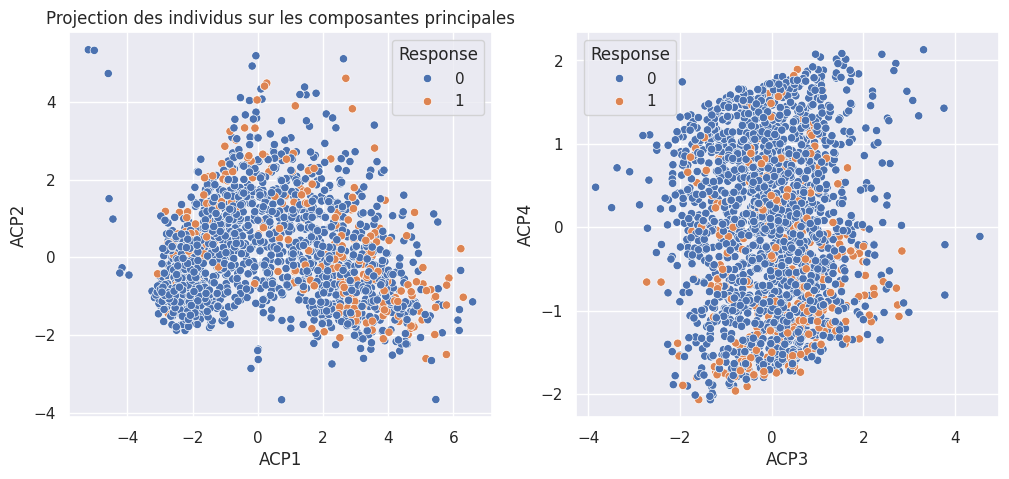
_, ax = plt.subplots(1, 2, figsize=(12, 5))

ax[0].set_title("Projection des individus sur les composantes principales")
sns.scatterplot(
    composantes_principales, x="ACP1", y="ACP2", hue=df["Response"], ax=ax[0]
)
sns.scatterplot(
    composantes_principales, x="ACP3", y="ACP4", hue=df["Response"], ax=ax[1]
)

<Axes: xlabel='ACP3', ylabel='ACP4'>

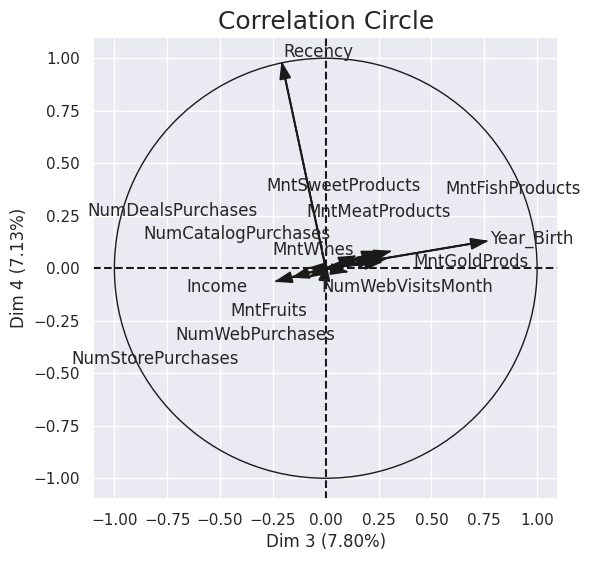
Cercle de corrélations

plot_pca_correlation_graph(
    df_centre_reduit,
    df_centre_reduit.columns,
    X_pca=composantes_principales.iloc[:, :2],
    explained_variance=acp.explained_variance_[:2],
    dimensions=(1, 2),
)

(<Figure size 600x600 with 1 Axes>,
                         Dim 1     Dim 2
 Year_Birth          -0.165705 -0.261059
 Income               0.854372 -0.032168
 Recency              0.010637  0.004087
 MntWines             0.751883  0.285810
 MntFruits            0.708341 -0.175398
 MntMeatProducts      0.798662 -0.175350
 MntFishProducts      0.732041 -0.180784
 MntSweetProducts     0.706228 -0.140825
 MntGoldProds         0.575925  0.238082
 NumDealsPurchases   -0.095773  0.772308
 NumWebPurchases      0.549861  0.602148
 NumCatalogPurchases  0.815305  0.018713
 NumStorePurchases    0.746004  0.225954
 NumWebVisitsMonth   -0.639886  0.488683)

_, correlation_matrix = plot_pca_correlation_graph(
    df_centre_reduit,
    df_centre_reduit.columns,
    X_pca=composantes_principales.iloc[:, :4],
    explained_variance=acp.explained_variance_[:4],
    dimensions=(3, 4),
)

plt.figure(figsize=(8, 6))
sns.heatmap(
    correlation_matrix,
    annot=True,
    cmap="BrBG",
    linewidths=0.5,
    vmax=1,
    vmin=-1,
)

<Axes: >

Tableau. Interprétation des 4 premiers axes de l’ACP

Axe	Interprétation
1	Richesse (revenu) Achats dans toutes les catégories Achats en catalogue et en magasin physique Peu de visites sur le site Internet
2	Achats en promotion
3	Année de naissance
4	Nombre de jours depuis le dernier achat (Recency)

Analyse Factorielle des Correspondances (AFC)

Kidhome vs Teenhome

table_contingence = pd.crosstab(df["Kidhome"], df["Teenhome"])

table_contingence

Teenhome	0	1	2
Kidhome
0	575	577	28
1	464	343	22
2	17	26	0

ca = prince.CA(random_state=seed)

ca = ca.fit(table_contingence)

ca.eigenvalues_summary

	eigenvalue	% of variance	% of variance (cumulative)
component
0	0.007	96.68%	96.68%
1	0.000	3.32%	100.00%

ca.plot(table_contingence)

Statut marital et niveau d’éducation

table_contingence = pd.crosstab(df["Marital_Status"], df["Education"])

table_contingence

Education	2n Cycle	Basic	Graduation	Master	PhD
Marital_Status
Divorced	21	1	113	33	47
Married	71	18	396	131	179
Single	37	18	234	69	93
Together	53	11	254	95	107
Widow	5	1	31	12	22

ca = prince.CA(random_state=seed)
ca = ca.fit(table_contingence)

ca.eigenvalues_summary

	eigenvalue	% of variance	% of variance (cumulative)
component
0	0.005	60.05%	60.05%
1	0.002	26.34%	86.39%

ca.plot(table_contingence)

## todo: à interpréter

Analyse des Correspondances Multiples (ACM)

Variables qualitatives uniquement

df["HasAcceptedCampaigns"] = df["HasAcceptedCampaigns"].astype(int)

mca = prince.MCA(
    n_components=df[var_categoriques_fe].shape[1],
    random_state=seed,
)
mca = mca.fit(df[var_categoriques_fe])

composantes_acm = mca.row_coordinates(df[var_categoriques_fe])
composantes_acm.columns = [f"ACM{i+1}" for i in range(composantes_acm.shape[1])]

mca.plot(df[var_categoriques_fe])

Tableau. Interprétation des 2 premiers axes de l’ACM

Axe	Interprétation
1	Nombre de campagnes acceptées Peu d’enfants
2	Niveau d’éducation faible

mca.plot(df[var_categoriques_fe], x_component=2, y_component=3)

Avec variables quantitatives en supplémenaire

mca.plot(df[var_categoriques_fe + var_numeriques])

## todo: à interpréter

Essai sans Education

mca = prince.MCA(random_state=seed)
mca = mca.fit(df[var_categoriques_fe].drop(columns=["Education"]))

mca.plot(df[var_categoriques_fe].drop(columns=["Education"]))

Sauvegarde des données

composantes_principales.to_csv(f"{data_folder}/composantes_acp.csv")
composantes_acm.to_csv(f"{data_folder}/composantes_acm.csv")