Clustering

Import des outils / jeu de données

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import prince
import seaborn as sns
from sklearn.cluster import (
    DBSCAN,
    OPTICS,
    AffinityPropagation,
    AgglomerativeClustering,
    KMeans,
    MeanShift,
)
from sklearn.compose import ColumnTransformer
from sklearn.metrics import (
    calinski_harabasz_score,
    davies_bouldin_score,
    silhouette_score,
)
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import RobustScaler, StandardScaler

from src.clustering import initiate_cluster_models
from src.config import data_folder, seed
from src.constants import var_categoriques, var_numeriques
from src.utils import init_notebook

init_notebook()

df = pd.read_csv(
    f"{data_folder}/data-cleaned-feature-engineering.csv",
    sep=",",
    index_col="ID",
    parse_dates=True,
)

composantes_acp = pd.read_csv(f"{data_folder}/composantes_acp.csv", index_col="ID")
composantes_acm = pd.read_csv(f"{data_folder}/composantes_acm.csv", index_col="ID")

Variables globales

var_categoriques_extra = ["NbAcceptedCampaigns", "HasAcceptedCampaigns", "NbChildren"]

var_categoriques_fe = var_categoriques + var_categoriques_extra

Clustering

Préparation des données

Nous commencer par fusionner les variables quantitatives et les coordonnées des individus dans l’ACM.

X_clust = pd.concat((df[var_numeriques], composantes_acm), axis=1)

X_clust.head()

	Year_Birth	Income	Recency	MntWines	MntFruits	MntMeatProducts	MntFishProducts	MntSweetProducts	MntGoldProds	NumDealsPurchases	...	ACM4	ACM5	ACM6	ACM7	ACM8	ACM9	ACM10	ACM11	ACM12	ACM13
ID
5524	1957	58138.0	58	635	88	546	172	88	88	3	...	-0.909429	0.439397	0.662880	-0.292805	-0.039068	0.196400	-0.843529	-0.898797	0.174169	0.960631
2174	1954	46344.0	38	11	1	6	2	1	6	2	...	-0.402198	0.129620	0.171945	-0.143049	-0.116974	0.105742	0.259841	0.262817	-0.093681	0.033373
4141	1965	71613.0	26	426	49	127	111	21	42	1	...	-0.423124	-0.465975	0.553202	0.541437	-1.880626	0.028891	-0.374510	-0.919603	0.287754	-0.350058
6182	1984	26646.0	26	11	4	20	10	3	5	2	...	-0.275507	-0.245603	0.246638	0.239619	-0.942750	-0.002593	-0.333331	0.052414	-0.412546	-0.177088
5324	1981	58293.0	94	173	43	118	46	27	15	5	...	0.554819	0.142063	-0.591854	-0.680550	0.175540	-0.518129	-0.348914	0.007669	-0.491990	-0.319610

5 rows × 27 columns

preprocessor = ColumnTransformer(
    remainder="passthrough",
    transformers=[
        ("scaler", RobustScaler(), var_numeriques),
    ],
)

scaler = RobustScaler()
df_apres_scale = pd.DataFrame(
    preprocessor.fit_transform(X_clust),
    columns=X_clust.columns,
    index=df.index,
)

df_apres_scale.head()

	Year_Birth	Income	Recency	MntWines	MntFruits	MntMeatProducts	MntFishProducts	MntSweetProducts	MntGoldProds	NumDealsPurchases	...	ACM4	ACM5	ACM6	ACM7	ACM8	ACM9	ACM10	ACM11	ACM12	ACM13
ID
5524	-0.722222	0.187662	0.18	0.957469	2.50000	2.238318	3.386243	2.424242	1.361702	0.5	...	-0.909429	0.439397	0.662880	-0.292805	-0.039068	0.196400	-0.843529	-0.898797	0.174169	0.960631
2174	-0.888889	-0.175314	-0.22	-0.337137	-0.21875	-0.285047	-0.211640	-0.212121	-0.382979	0.0	...	-0.402198	0.129620	0.171945	-0.143049	-0.116974	0.105742	0.259841	0.262817	-0.093681	0.033373
4141	-0.277778	0.602373	-0.46	0.523859	1.28125	0.280374	2.095238	0.393939	0.382979	-0.5	...	-0.423124	-0.465975	0.553202	0.541437	-1.880626	0.028891	-0.374510	-0.919603	0.287754	-0.350058
6182	0.777778	-0.781546	-0.46	-0.337137	-0.12500	-0.219626	-0.042328	-0.151515	-0.404255	0.0	...	-0.275507	-0.245603	0.246638	0.239619	-0.942750	-0.002593	-0.333331	0.052414	-0.412546	-0.177088
5324	0.611111	0.192433	0.90	-0.001037	1.09375	0.238318	0.719577	0.575758	-0.191489	1.5	...	0.554819	0.142063	-0.591854	-0.680550	0.175540	-0.518129	-0.348914	0.007669	-0.491990	-0.319610

5 rows × 27 columns

df_avec_clusters = df_apres_scale.copy()

Différents algorithmes de clustering

Nous choisissons de tester 2 types de modèles de clustering :

1. les modèles à choix du nombre de clusters

2. les modèles qui décident du nombre de clusters

Cela nous permettra de comparer le nombre de clusters donné par les seconds algorithmes.

Pour les modèles pour lesquels il faut choisir le nombre de clusters, nous décidons de tester des clusters de taille 2 à 5 (inclus), car un trop grand nombre de clusters serait plus difficile à interpréter pour l’équipe marketing dans un premier temps.

Tableau. Méthodologie de clustering

|:—————————-|:—-| | Algorithmes | Avec choix du nombre de clusters (entre 2 et 5)
Sans choix du nombre de clusters | | Critères de sélection | Répartition des clusters
Métriques de clusters
Sélection manuelle des clusters via leur affichage | | Métriques | Score Silhouette (entre -1 et 1, proche de 1 = meilleurs clusters)
Calinski-Harabasz (entre 0 et $+\infty$ plus grand = meilleure séparation)
Davies-Bouldin (entre 0 et $+\infty$, proche de 0 = meilleurs clusters) | | Affichage des clusters | Sur les axes d’ACP 1-4
Sur les axes d’ACM 1-4
En fonction des variables quantitatives
En fonction des variables qualitatives |

Tableau. Algorithmes de clustering testés

Choix du nombre de clusters	Algorithmes
Avec	KMeans Mélange Gaussien (GMM) Classification Ascendante Hiérarchique (CAH) (méthode de Ward, single/complete/average linkage)
Sans	OPTICS Mean Shift Propagation d’affinité (Affinity Propagation)

NB_CLUSTER_MIN = 2
NB_CLUSTER_MAX = 6  ## non inclus

model_clusters = initiate_cluster_models(
    NB_CLUSTER_MIN,
    NB_CLUSTER_MAX,
    seed,
)

a = GaussianMixture()

isinstance(a, GaussianMixture)

True

cluster_metrics = []

for (model_name, model) in model_clusters.items():
    if isinstance(model, GaussianMixture):  ## cas particulier du mélange gaussien
        df_avec_clusters[model_name] = model.fit_predict(df_apres_scale)
    else:
        model.fit(df_apres_scale)
        df_avec_clusters[model_name] = model.labels_

    df_avec_clusters[model_name] = pd.Categorical(
        df_avec_clusters[model_name].astype(str)
    )

    nb_clusters = df_avec_clusters[model_name].nunique()

    repartition = list(
        df_avec_clusters[model_name].value_counts(normalize=True).round(2).astype(str)
    )  ## todo: enlever astype(str) si ça sert à rien (tester)

    cluster_metrics.append(
        [
            model_name,
            nb_clusters,
            " | ".join(repartition),
            silhouette_score(
                df_apres_scale, df_avec_clusters[model_name], random_state=seed
            ),  ## proche de 1 = mieux
            calinski_harabasz_score(
                df_apres_scale,
                df_avec_clusters[model_name],
            ),  ## plus élevé, mieux c'est
            davies_bouldin_score(
                df_apres_scale, df_avec_clusters[model_name]
            ),  ## proche de 0 = mieux
        ]
    )

/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:1416: FutureWarning: The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning
  super()._check_params_vs_input(X, default_n_init=10)

/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:1416: FutureWarning: The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning
  super()._check_params_vs_input(X, default_n_init=10)

/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:1416: FutureWarning: The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning
  super()._check_params_vs_input(X, default_n_init=10)

/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/sklearn/cluster/_kmeans.py:1416: FutureWarning: The default value of `n_init` will change from 10 to 'auto' in 1.4. Set the value of `n_init` explicitly to suppress the warning
  super()._check_params_vs_input(X, default_n_init=10)

/home/runner/.cache/pypoetry/virtualenvs/customer-base-analysis-F-W2gxNr-py3.10/lib/python3.10/site-packages/sklearn/cluster/_affinity_propagation.py:142: ConvergenceWarning: Affinity propagation did not converge, this model may return degenerate cluster centers and labels.
  warnings.warn(

pd.DataFrame(
    cluster_metrics,
    columns=[
        "Algorithme de clustering",
        "Nombre de clusters",
        "Répartition",
        "Silhouette",
        "Calinski-Harabasz",
        "Davies-Bouldin",
    ],
)

	Algorithme de clustering	Nombre de clusters	Répartition	Silhouette	Calinski-Harabasz	Davies-Bouldin
0	KMeans2	2	0.68 | 0.32	0.318482	754.878090	1.547400
1	KMeans3	3	0.46 | 0.29 | 0.25	0.167516	513.955410	1.982583
2	KMeans4	4	0.45 | 0.25 | 0.19 | 0.12	0.157546	402.274688	2.334645
3	KMeans5	5	0.44 | 0.23 | 0.19 | 0.12 | 0.02	0.170982	340.753601	2.058930
4	GMM2	2	0.52 | 0.48	0.207188	542.083968	1.740252
5	GMM3	3	0.52 | 0.31 | 0.18	0.062900	218.097499	3.099757
6	GMM4	4	0.36 | 0.3 | 0.27 | 0.06	0.087929	268.462211	4.010402
7	GMM5	5	0.43 | 0.34 | 0.13 | 0.07 | 0.02	0.129101	205.782852	3.352396
8	CAH (Ward) 2	2	0.72 | 0.28	0.314124	657.064212	1.618113
9	CAH (Ward) 3	3	0.44 | 0.28 | 0.28	0.138385	456.284028	2.071393
10	CAH (Ward) 4	4	0.41 | 0.28 | 0.28 | 0.02	0.147383	348.454297	1.794500
11	CAH (Ward) 5	5	0.41 | 0.28 | 0.22 | 0.06 | 0.02	0.142491	292.850286	2.186182
12	CAH (average linkage) 2	2	1.0 | 0.0	0.552208	29.958308	0.928812
13	CAH (average linkage) 3	3	1.0 | 0.0 | 0.0	0.523717	18.536309	0.735997
14	CAH (average linkage) 4	4	1.0 | 0.0 | 0.0 | 0.0	0.478857	14.305294	0.755391
15	CAH (average linkage) 5	5	1.0 | 0.0 | 0.0 | 0.0 | 0.0	0.458367	14.762254	0.896412
16	CAH (single linkage) 2	2	1.0 | 0.0	0.587091	26.332043	0.549969
17	CAH (single linkage) 3	3	1.0 | 0.0 | 0.0	0.568624	17.823639	0.468717
18	CAH (single linkage) 4	4	1.0 | 0.0 | 0.0 | 0.0	0.540606	14.538207	0.434358
19	CAH (single linkage) 5	5	1.0 | 0.0 | 0.0 | 0.0 | 0.0	0.518696	12.704006	0.417355
20	CAH (complete linkage) 2	2	1.0 | 0.0	0.552208	29.958308	0.928812
21	CAH (complete linkage) 3	3	1.0 | 0.0 | 0.0	0.540075	21.966639	0.879092
22	CAH (complete linkage) 4	4	0.72 | 0.27 | 0.0 | 0.0	0.317609	248.338621	1.259276
23	CAH (complete linkage) 5	5	0.71 | 0.27 | 0.01 | 0.0 | 0.0	0.290965	202.334927	1.242878
24	OPTICS	28	0.89 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01...	-0.295888	7.766509	1.447745
25	MeanShift	22	0.84 | 0.04 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01...	0.197199	42.398326	1.371609
26	AffinityPropagation	142	0.04 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02...	0.098856	40.876485	1.657521

Clusters sélectionnés :

• KMeans 2

• GMM 2

• CAH (Ward 2)

Nous avons aussi étudié certains clusters avec 3 groupes, qui nous ont permis d’identifier certains individus, mais qui ne sont pas aussi intéressants et utilisables que les clusters avec 2 groupes.

Visualisation

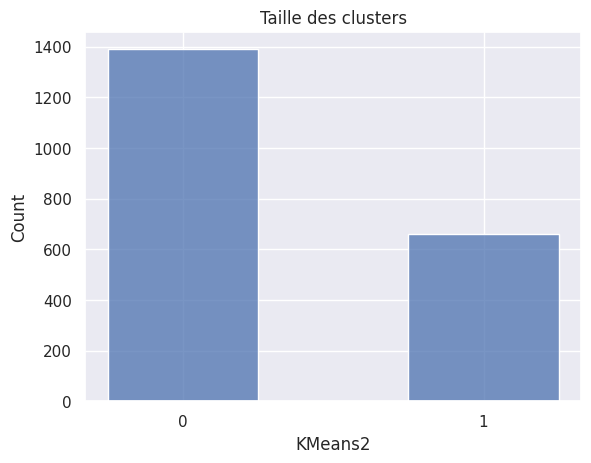
def affiche_taille_clusters(nom_cluster):
    plt.title("Taille des clusters")
    sns.histplot(df_avec_clusters[nom_cluster], shrink=0.5)

    plt.show()

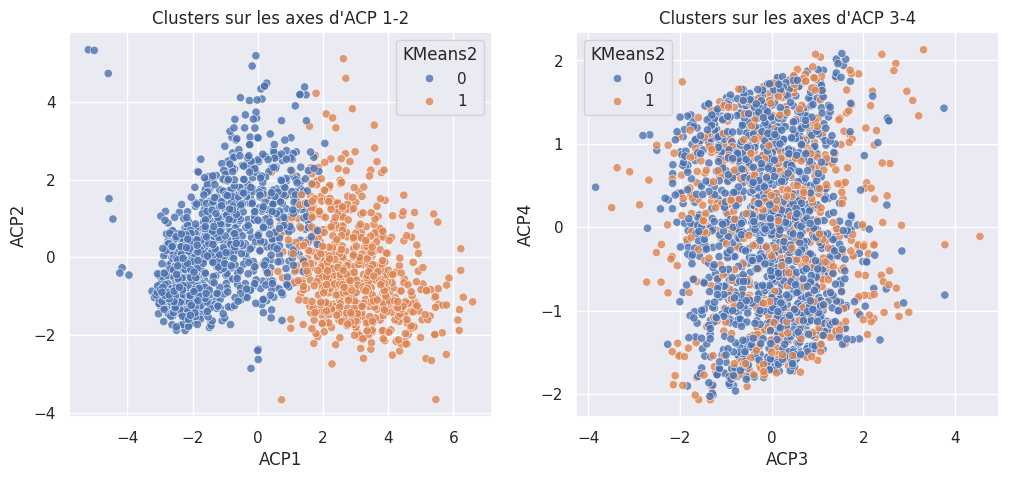
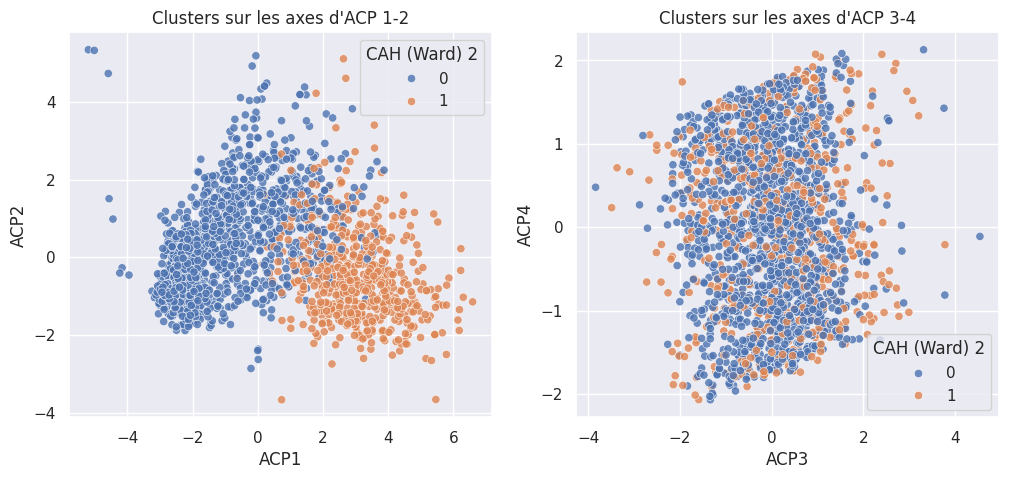
def affiche_clusters_acp(nom_cluster):
    _, ax = plt.subplots(1, 2, figsize=(12, 5))

    ax[0].set_title("Clusters sur les axes d'ACP 1-2")
    ax[1].set_title("Clusters sur les axes d'ACP 3-4")

    sns.scatterplot(
        composantes_acp,
        x="ACP1",
        y="ACP2",
        hue=df_avec_clusters[nom_cluster],
        alpha=0.8,
        ax=ax[0],
    )
    sns.scatterplot(
        composantes_acp,
        x="ACP3",
        y="ACP4",
        hue=df_avec_clusters[nom_cluster],
        alpha=0.8,
        ax=ax[1],
    )

    plt.show()

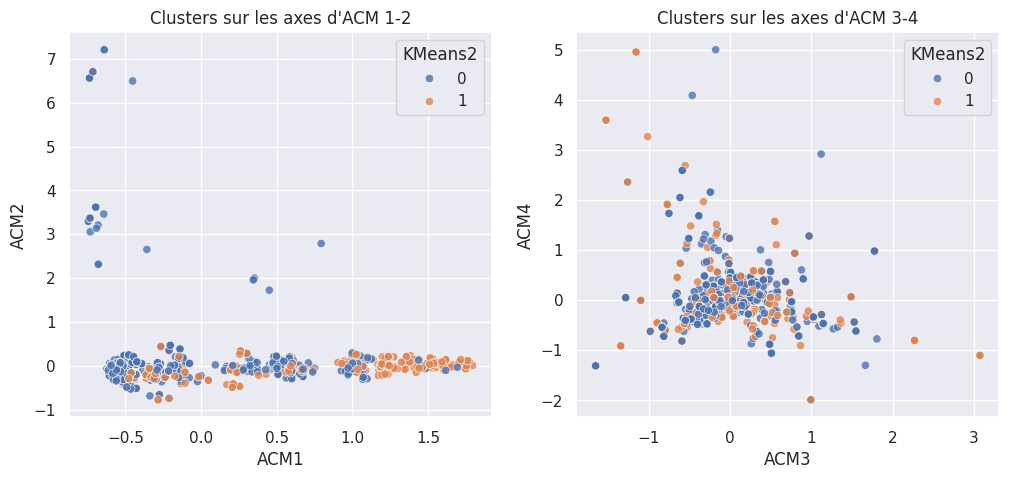
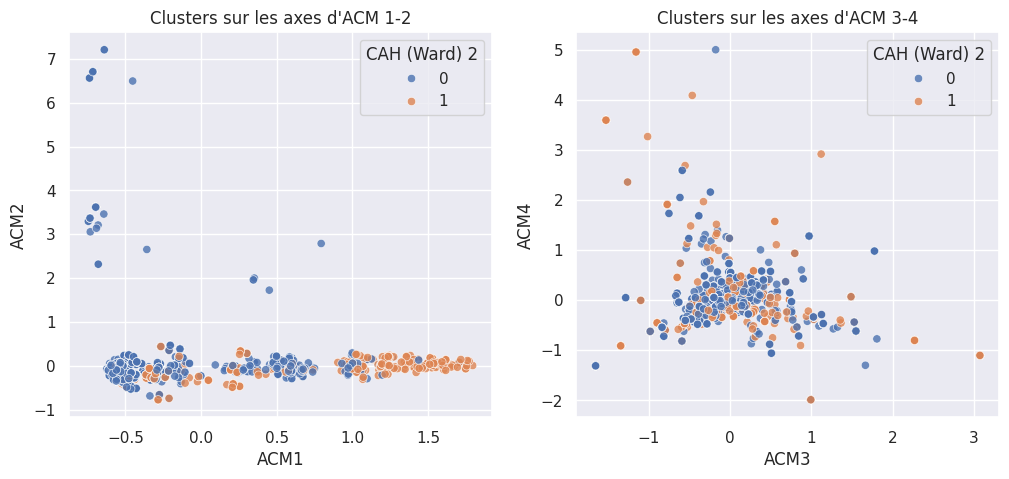
def affiche_clusters_acm(nom_cluster):
    _, ax = plt.subplots(1, 2, figsize=(12, 5))

    ax[0].set_title("Clusters sur les axes d'ACM 1-2")
    ax[1].set_title("Clusters sur les axes d'ACM 3-4")

    sns.scatterplot(
        composantes_acm,
        x="ACM1",
        y="ACM2",
        hue=df_avec_clusters[nom_cluster],
        alpha=0.8,
        ax=ax[0],
    )

    sns.scatterplot(
        composantes_acm,
        x="ACM3",
        y="ACM4",
        hue=df_avec_clusters[nom_cluster],
        alpha=0.8,
        ax=ax[1],
    )

    plt.show()

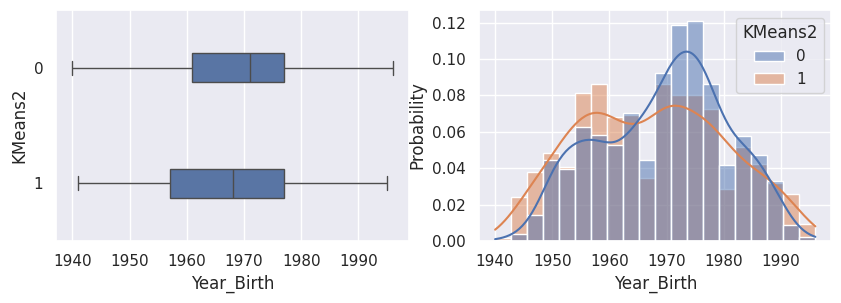
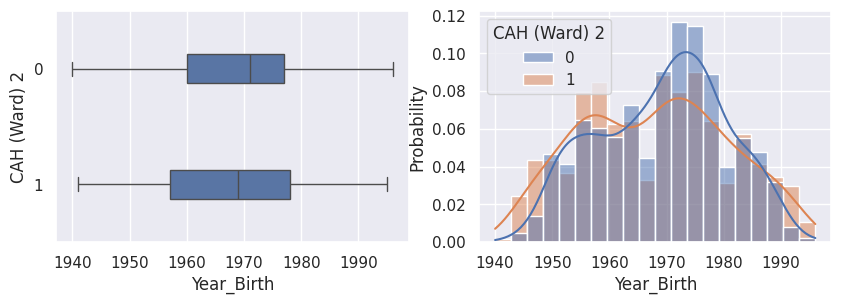
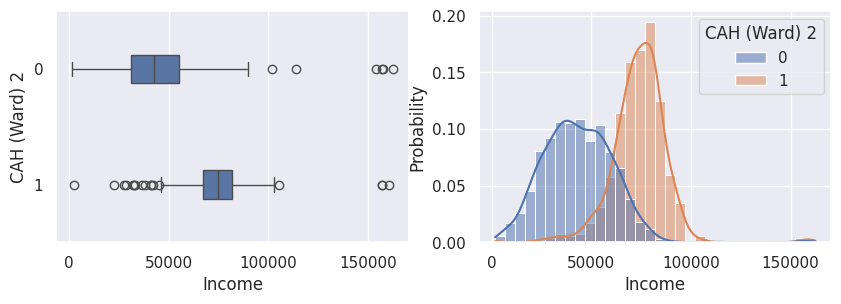
def affiche_clusters_var_quanti(nom_cluster):
    """Affiche les variables quantitatives en fonction des clusters."""
    for var in var_numeriques:
        _, ax = plt.subplots(1, 2, figsize=(10, 3))

        sns.boxplot(
            x=df[var],
            y=df_avec_clusters[nom_cluster],
            width=0.25,
            ax=ax[0],
        )

        sns.histplot(
            x=df[var],
            kde=True,
            ax=ax[1],
            hue=df_avec_clusters[nom_cluster],
            stat="probability",
            common_norm=False,
        )

        plt.show()

def affiche_clusters_var_quali(nom_cluster):
    """Affiche les variables qualitatives en fonction des clusters et vice-versa."""
    for var in var_categoriques_fe:
        _, ax = plt.subplots(1, 2, figsize=(10, 4))

        sns.histplot(
            x=df[var].astype(str),
            ax=ax[0],
            hue=df_avec_clusters[nom_cluster],
            multiple="dodge",
            shrink=0.5,
            common_norm=True,
        )

        sns.histplot(
            hue=df[var].astype(str),
            ax=ax[1],
            x=df_avec_clusters[nom_cluster],
            multiple="dodge",
            shrink=0.5,
            common_norm=True,
        )

        plt.show()

def affiche_clusters(nom_cluster):
    """Affiche les variables en fonction des clusters."""
    affiche_taille_clusters(nom_cluster)
    affiche_clusters_acp(nom_cluster)
    affiche_clusters_acm(nom_cluster)

    affiche_clusters_var_quanti(nom_cluster)
    affiche_clusters_var_quali(nom_cluster)

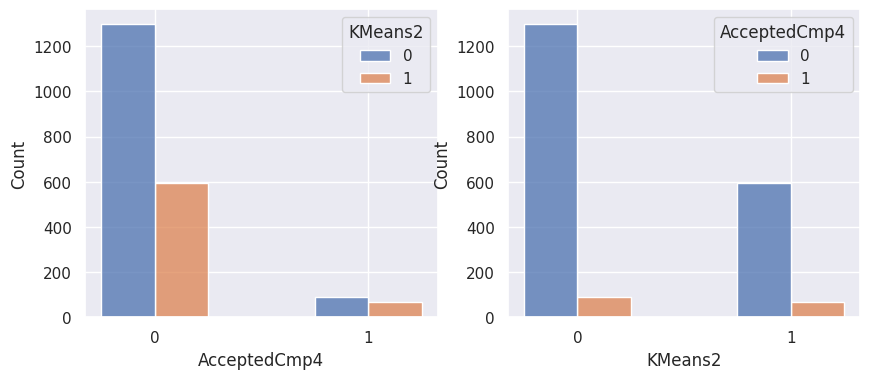
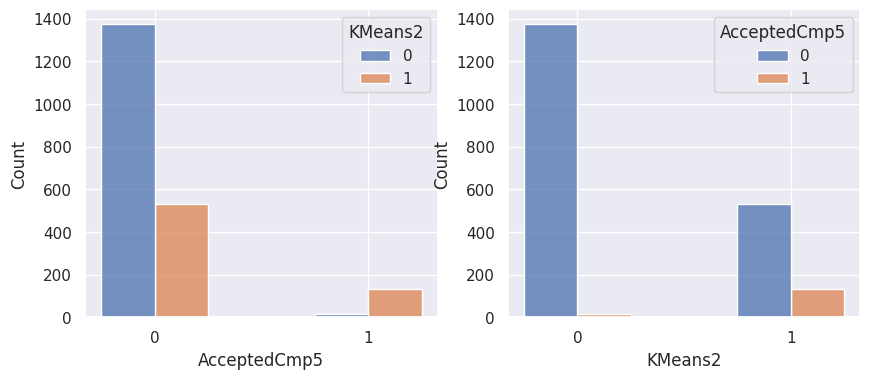
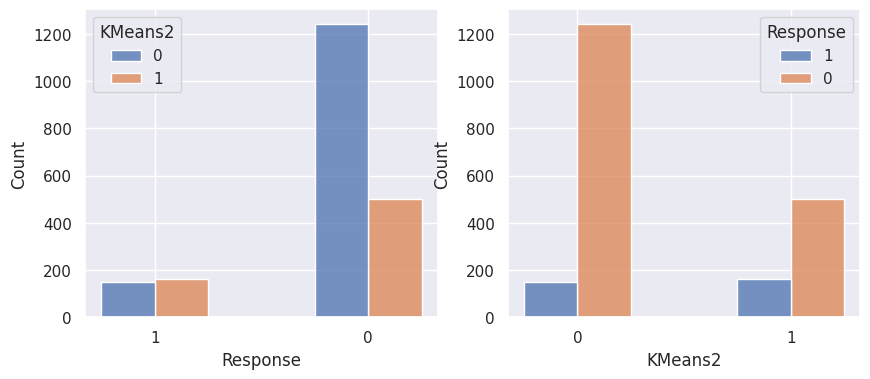
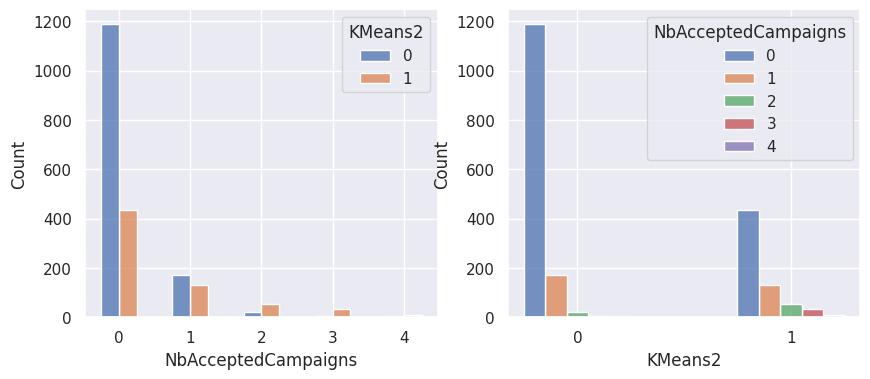
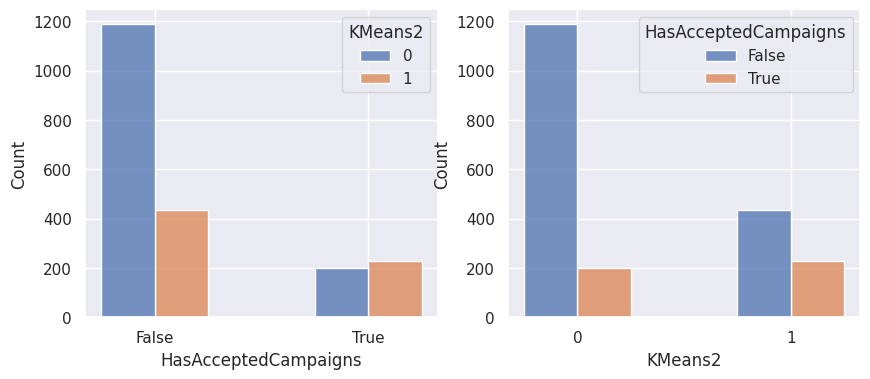
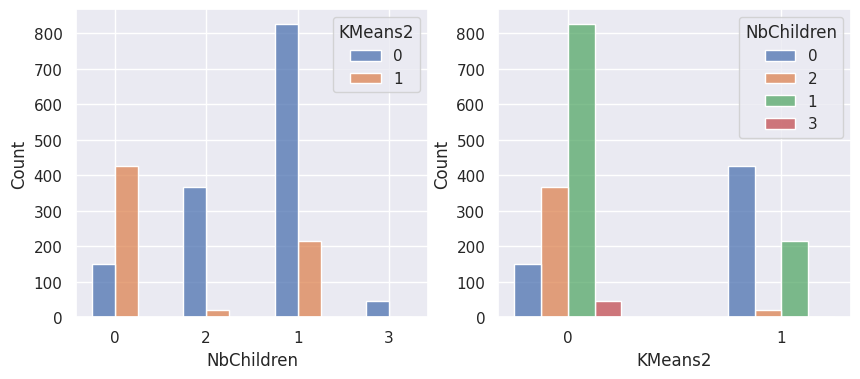
affiche_clusters("KMeans2")

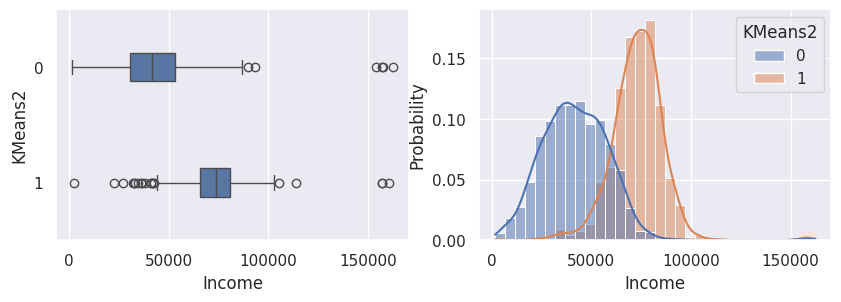
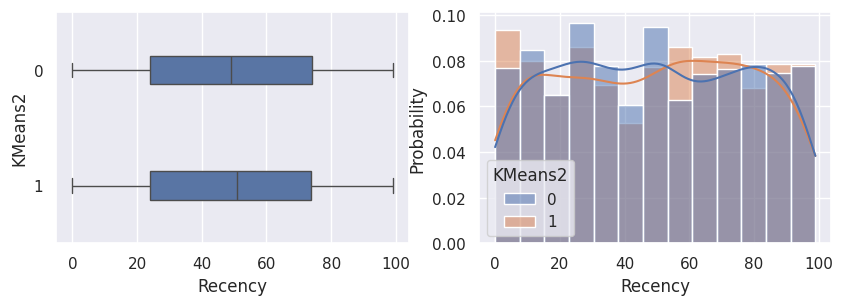
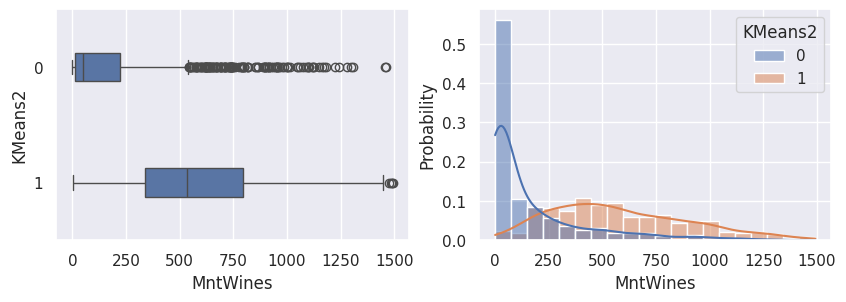
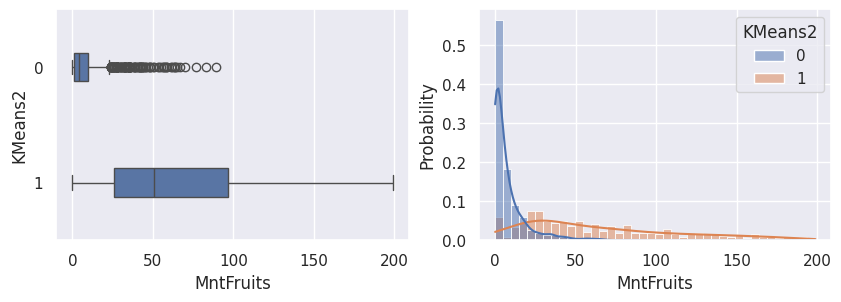
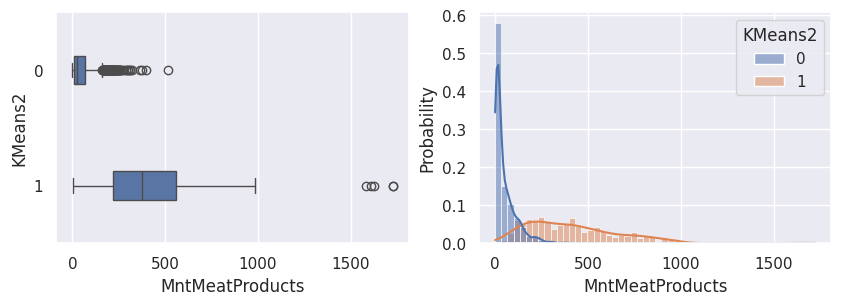
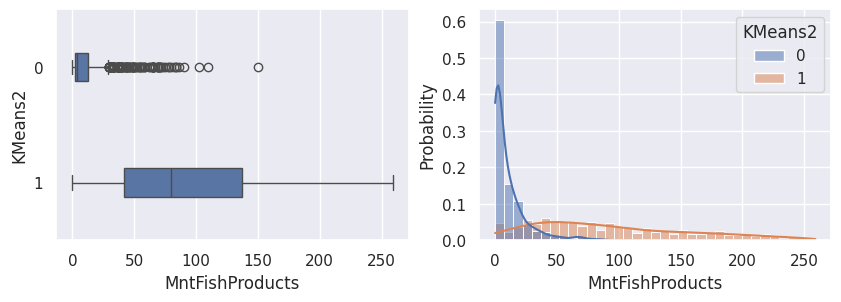
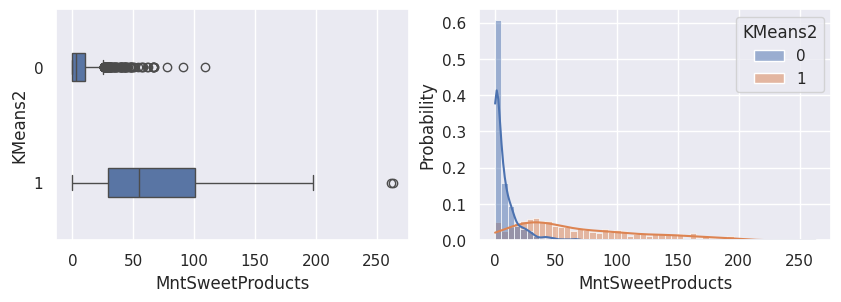
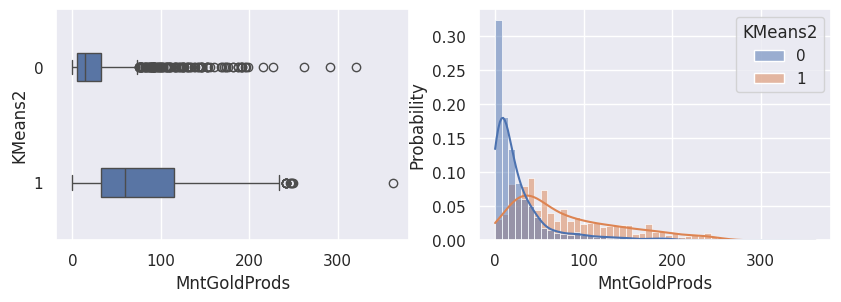
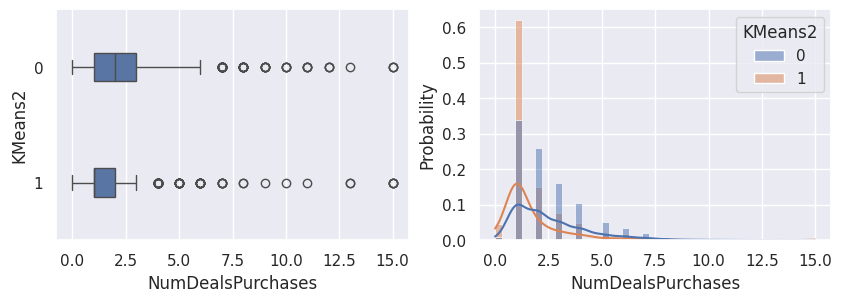
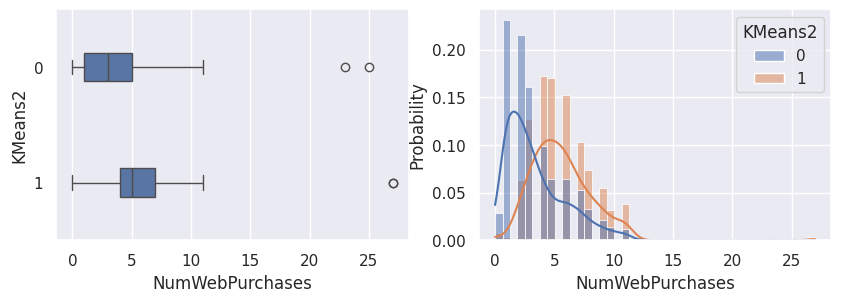
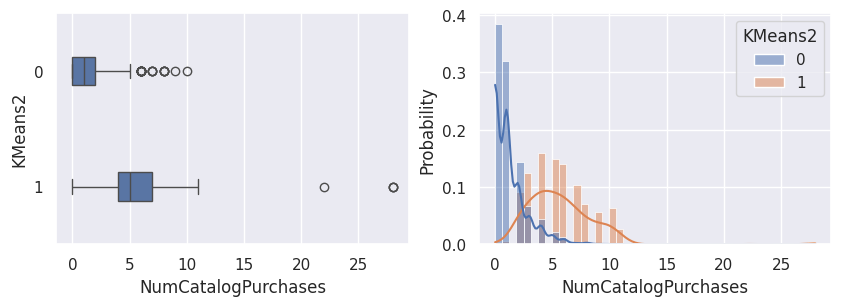
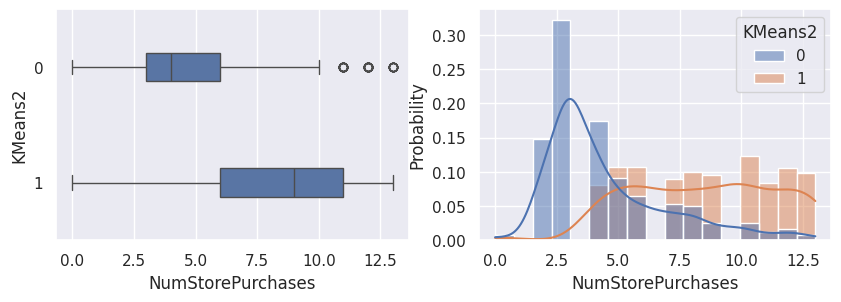
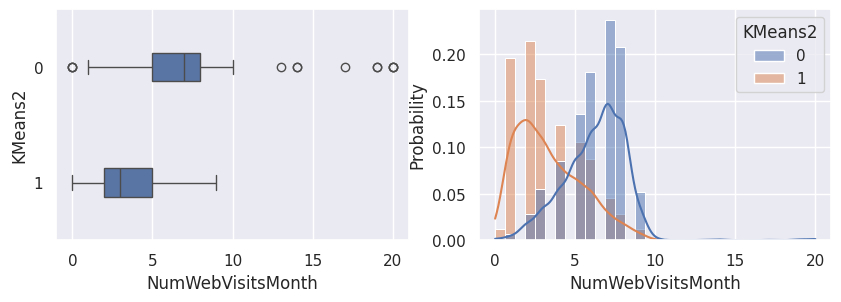
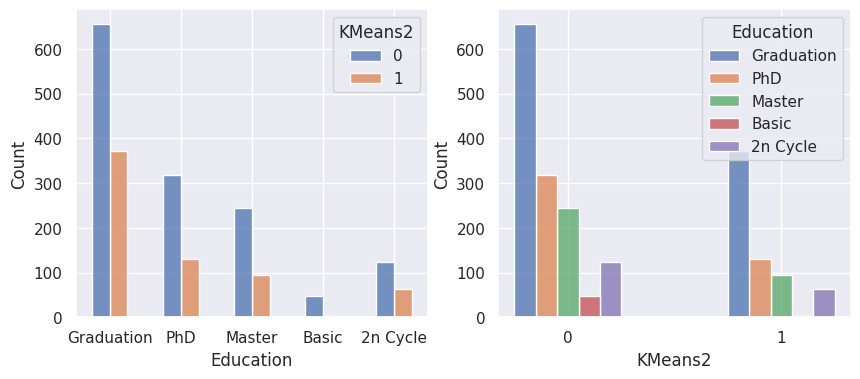
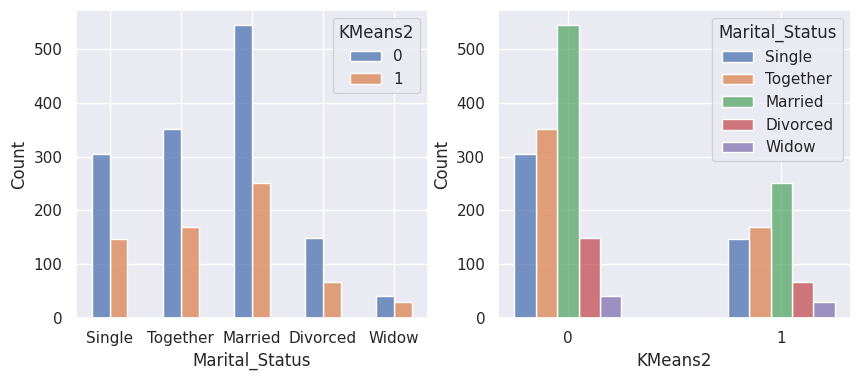
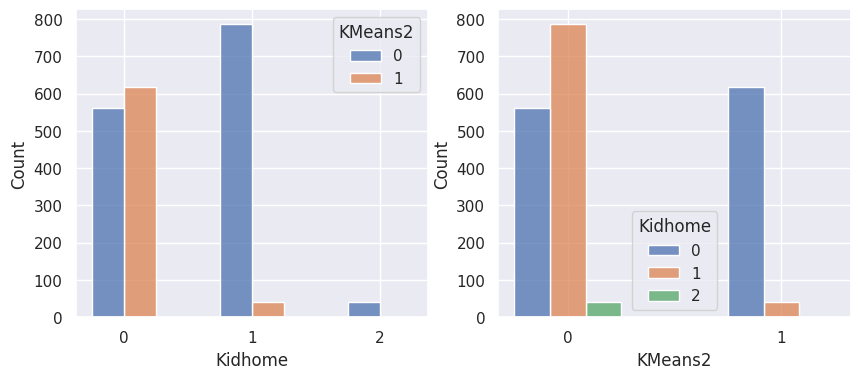
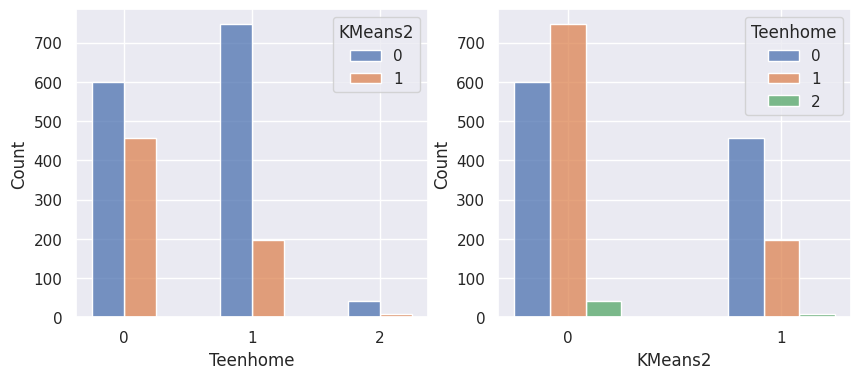
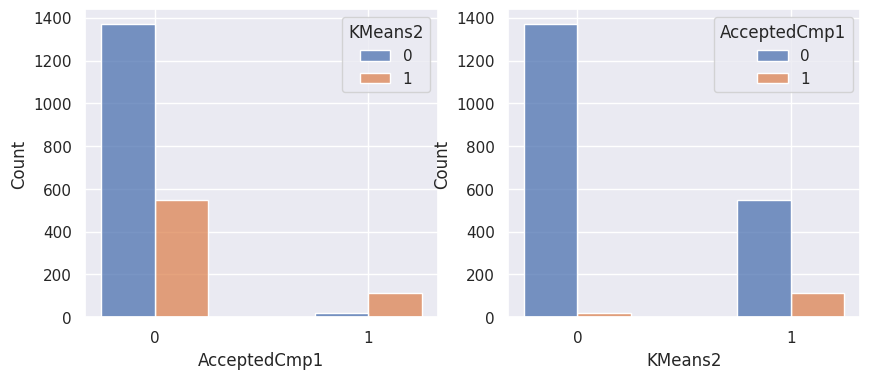
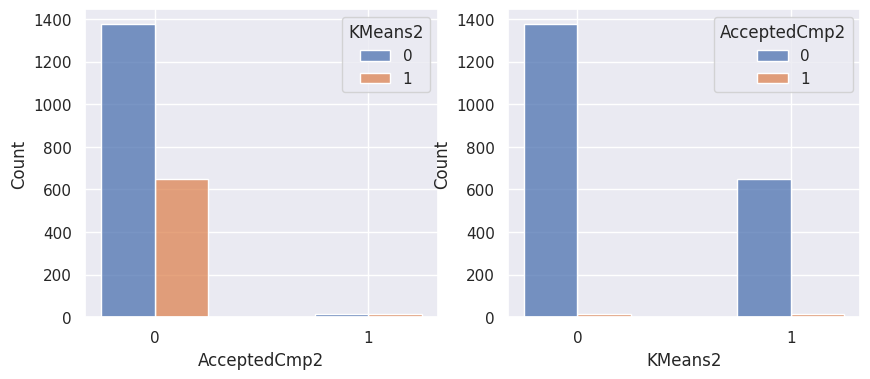
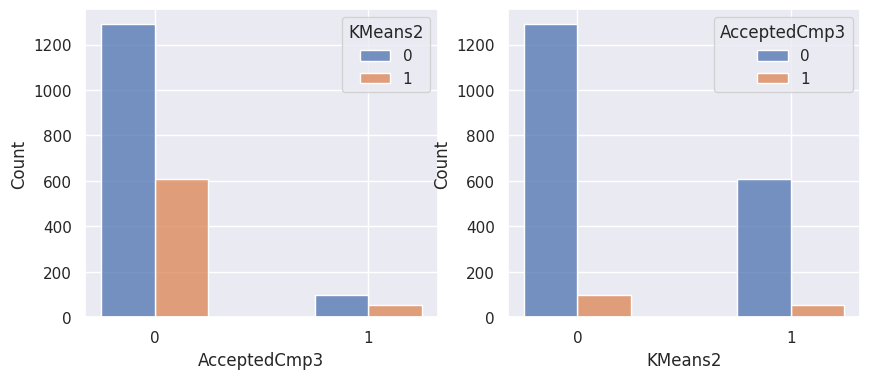
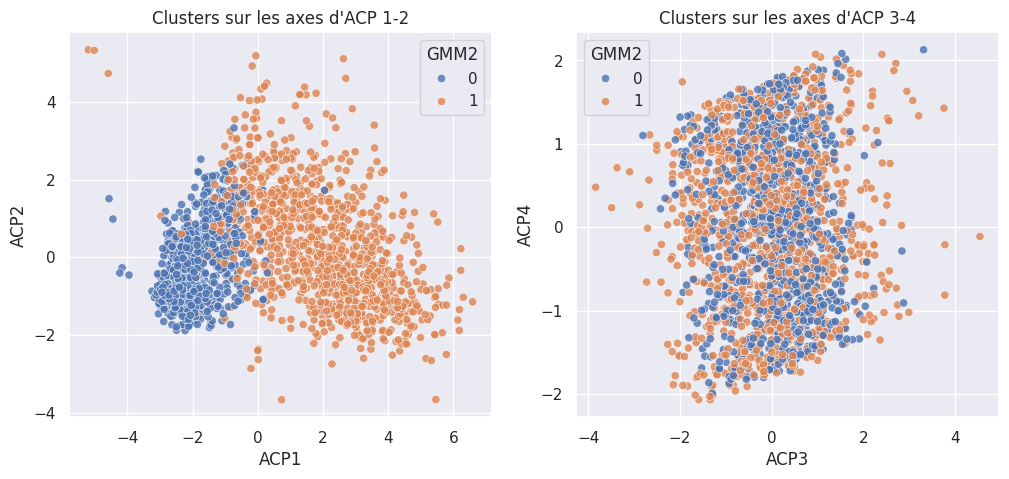
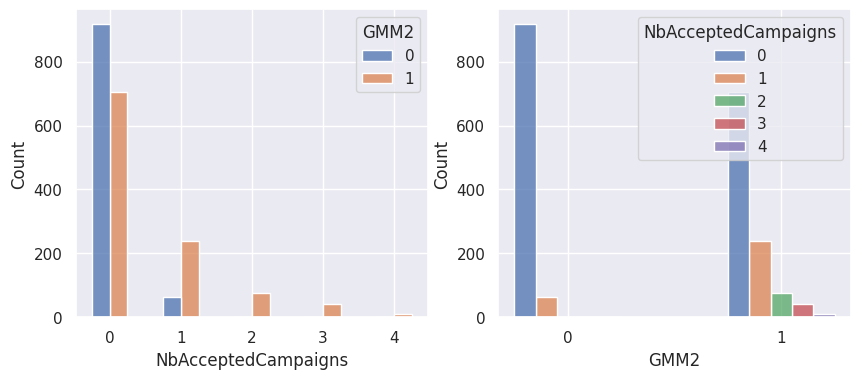
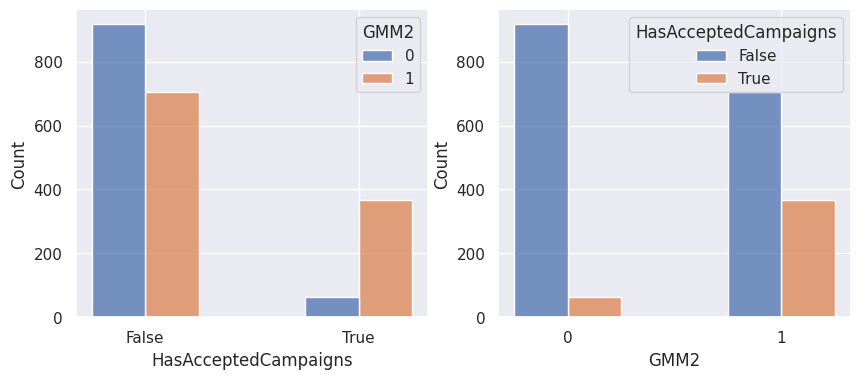
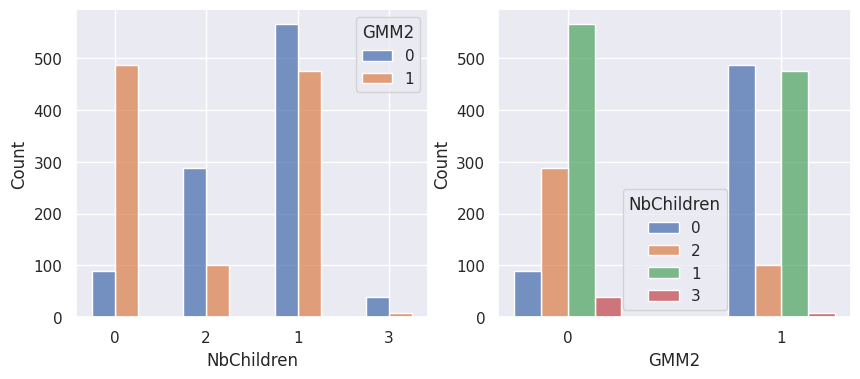
affiche_clusters("GMM2")

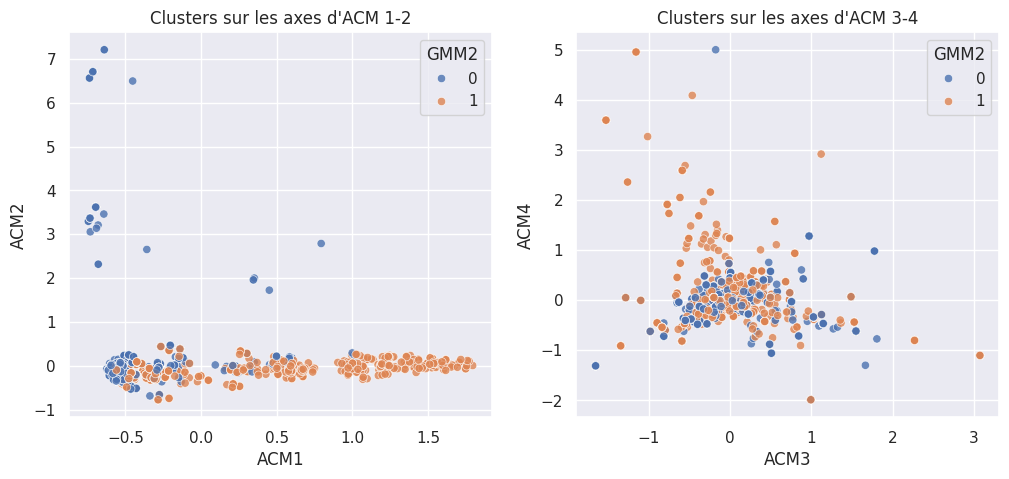
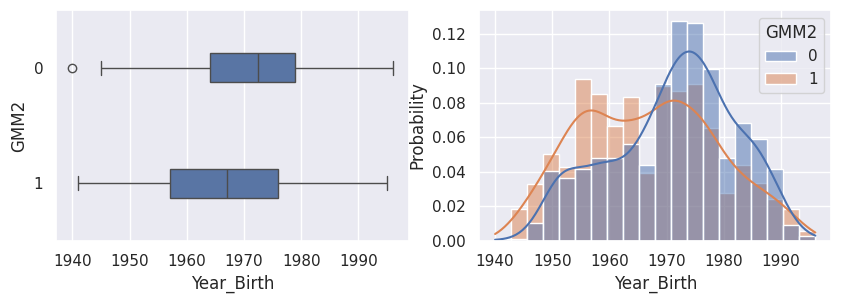
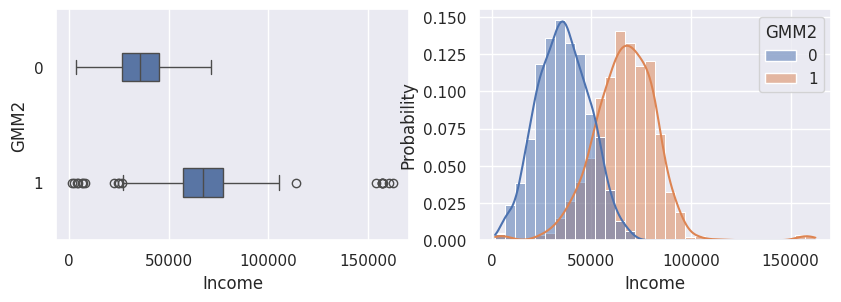
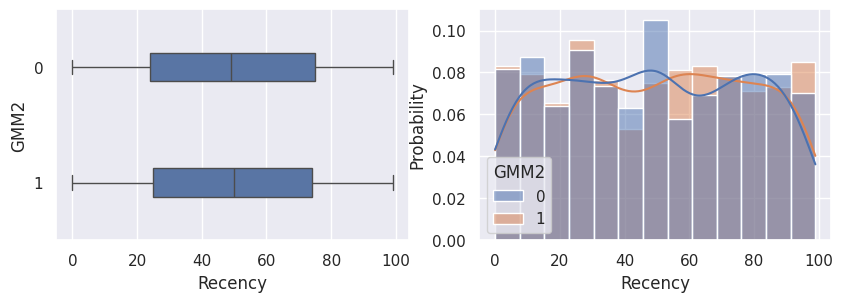
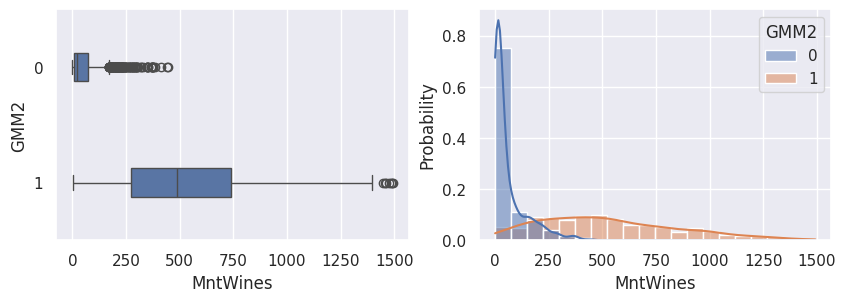
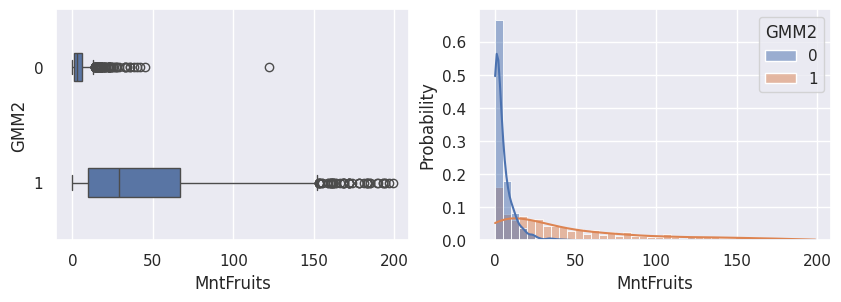
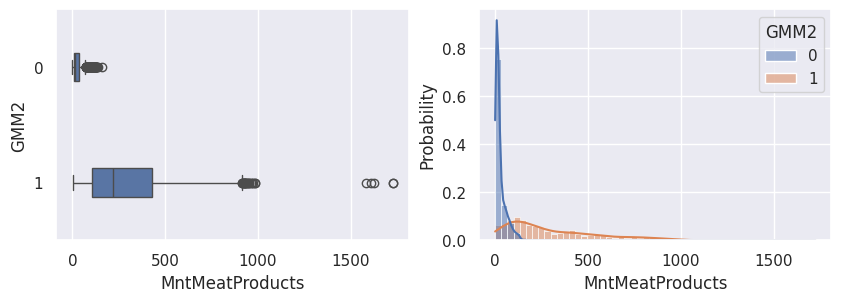
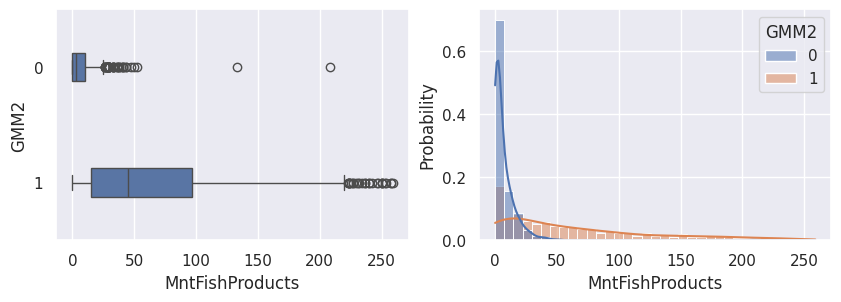
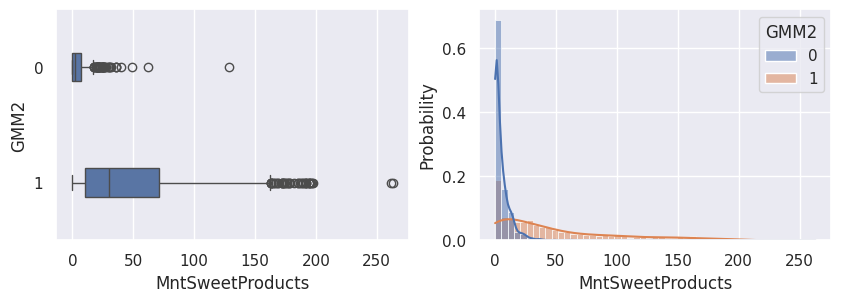
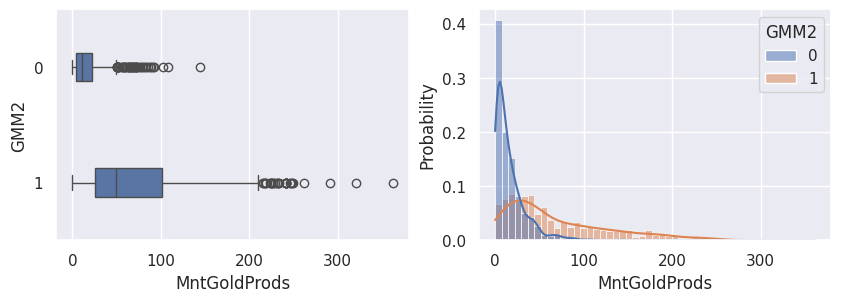
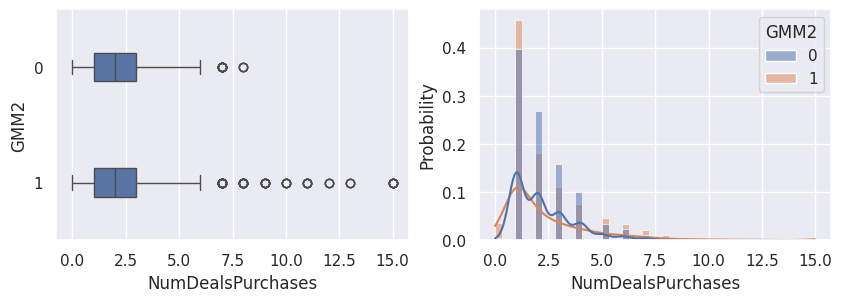
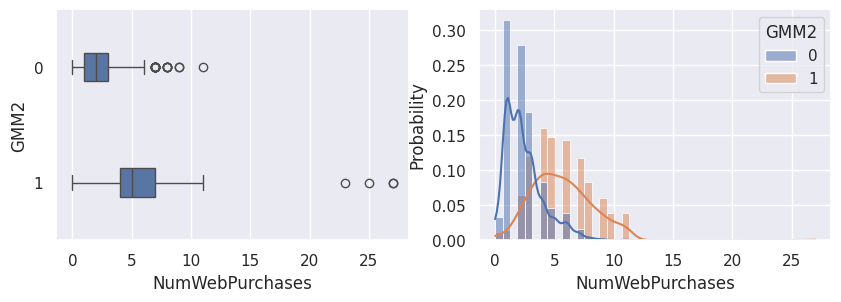
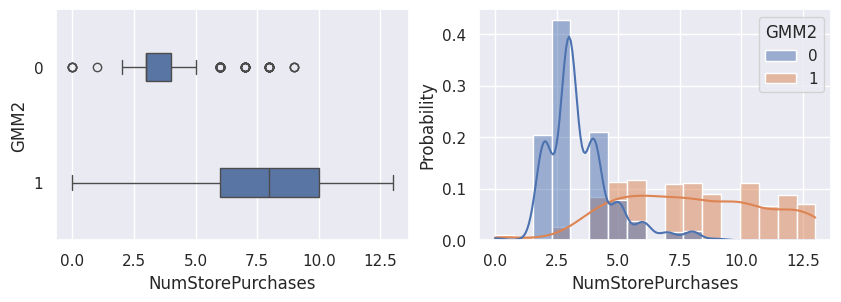
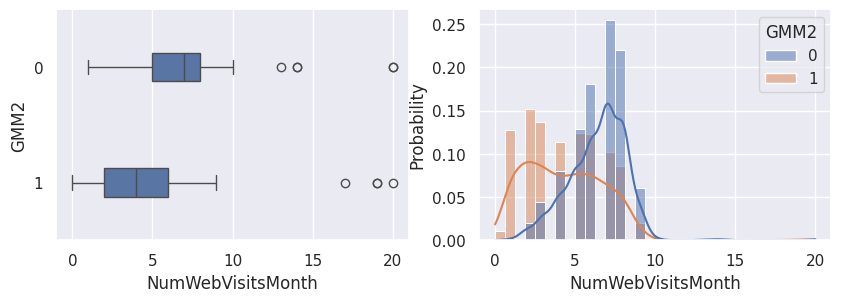
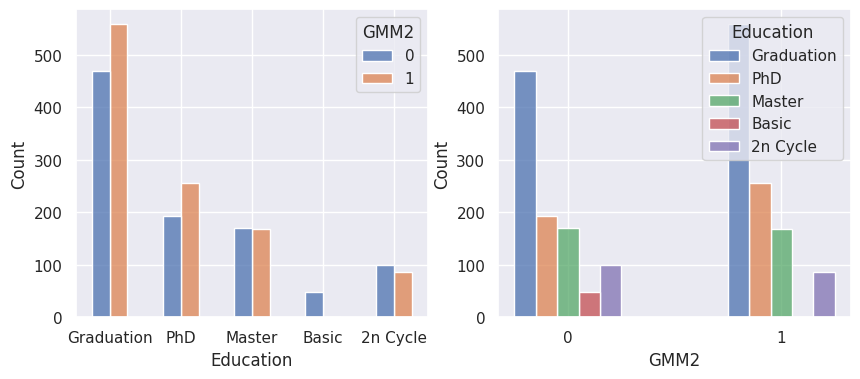
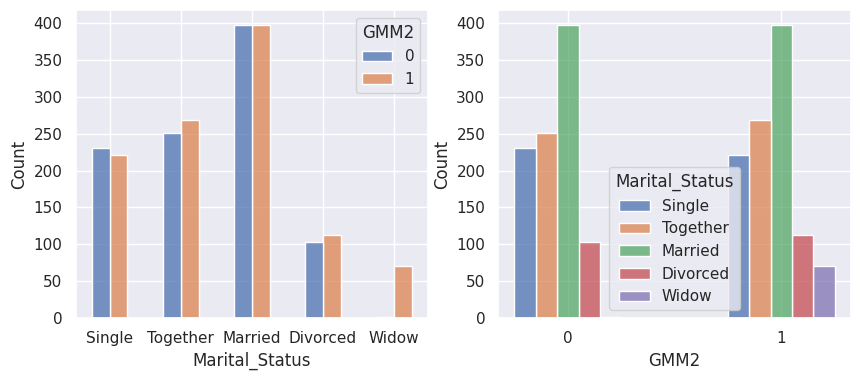
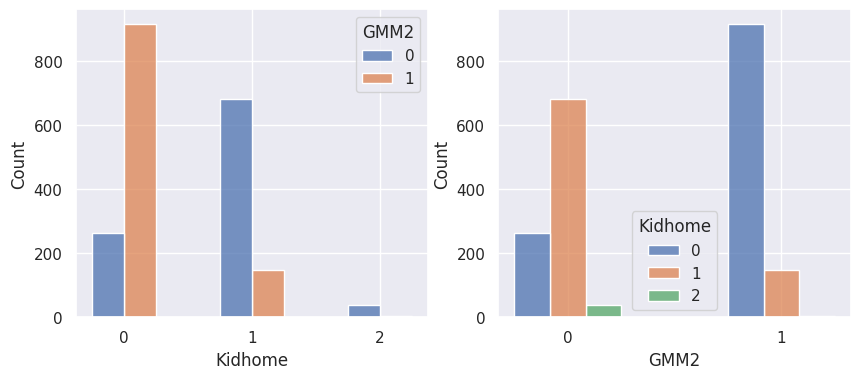
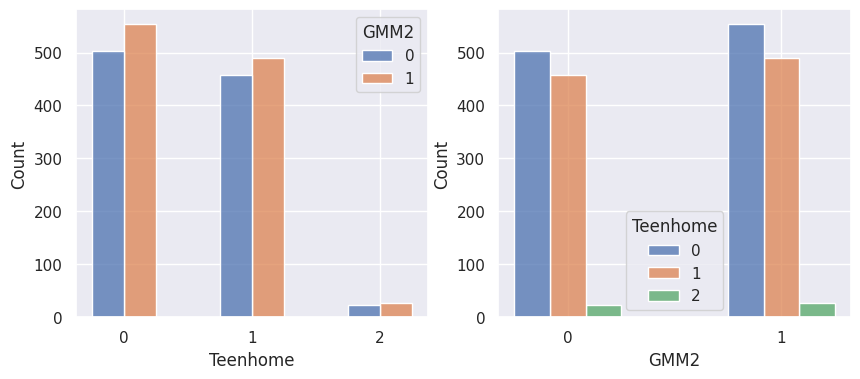
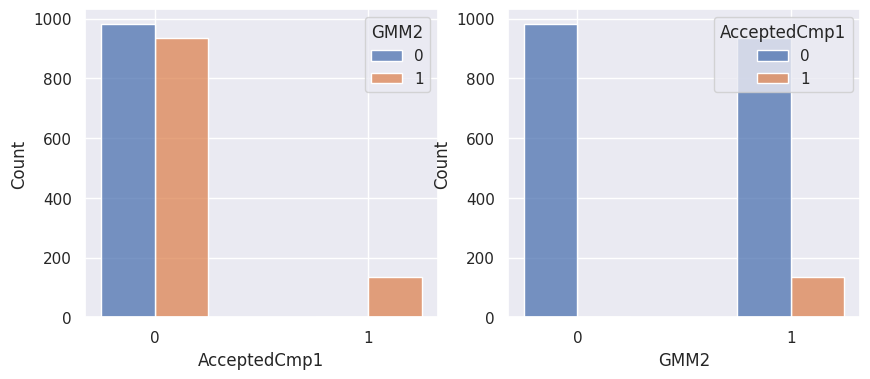
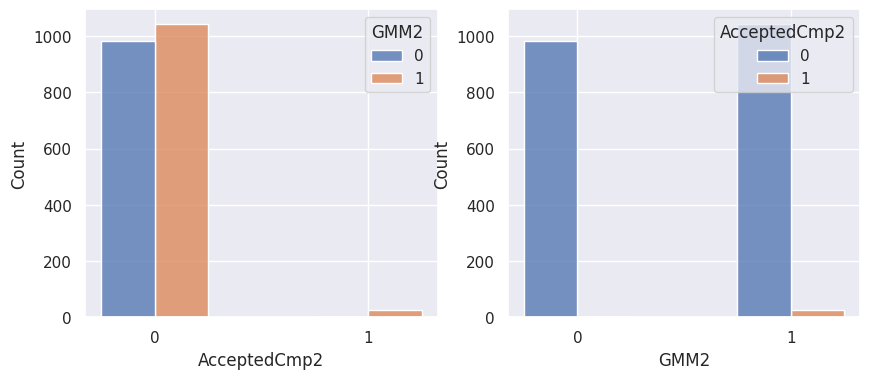
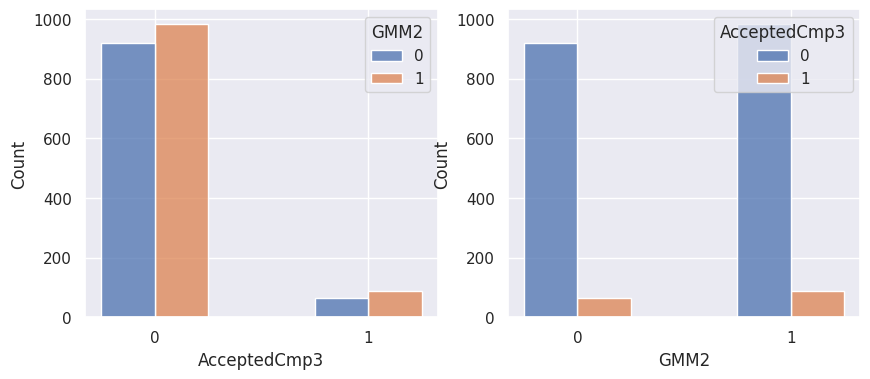
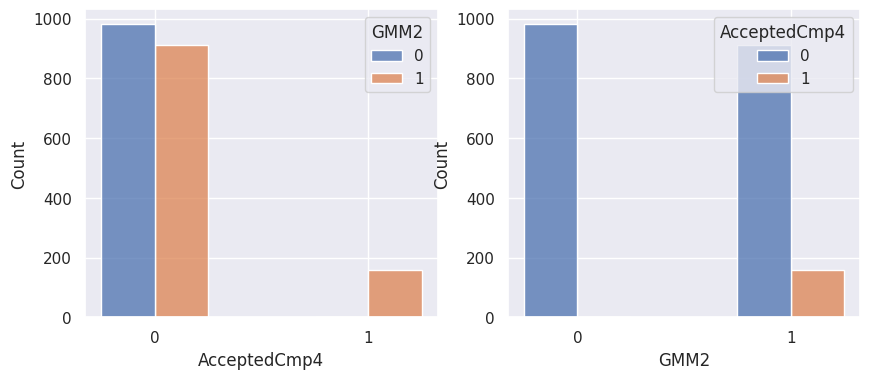
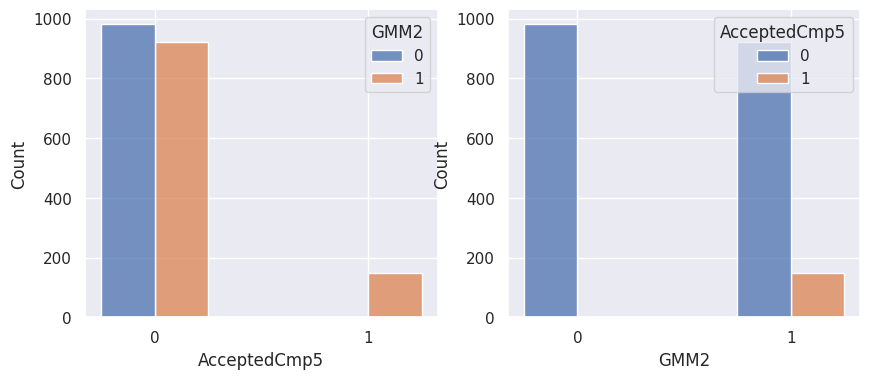
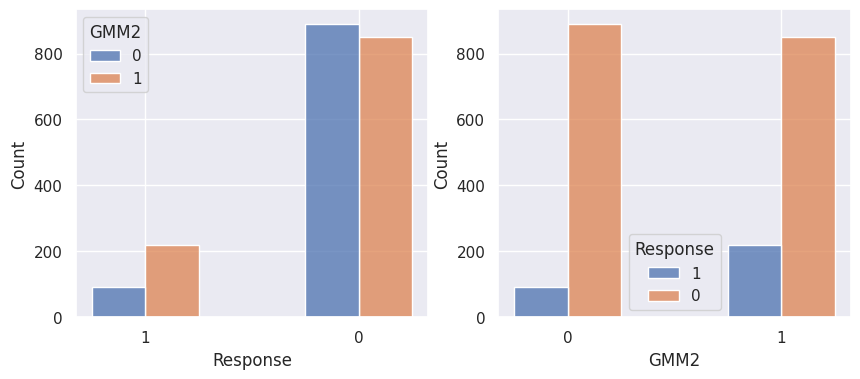
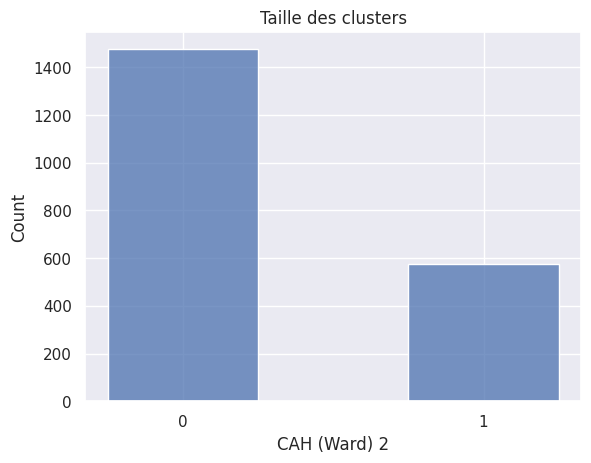
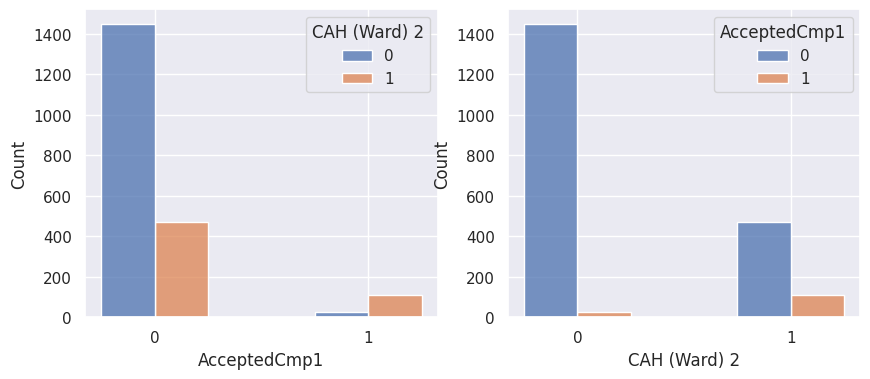
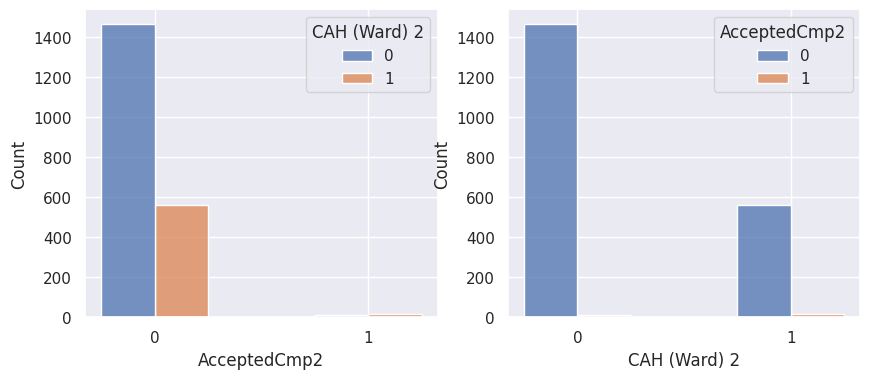
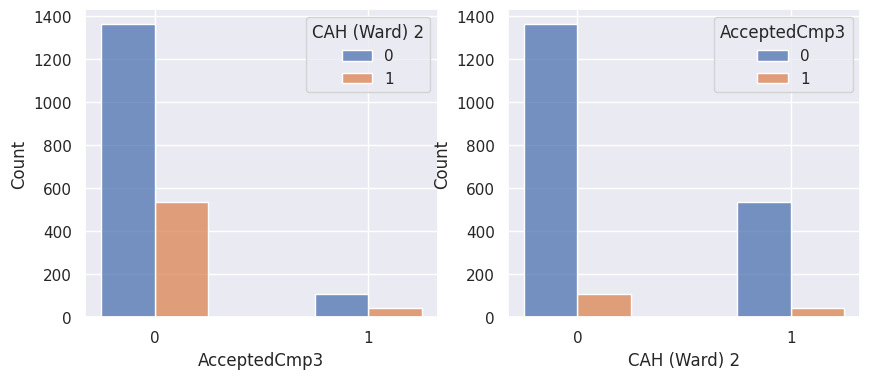
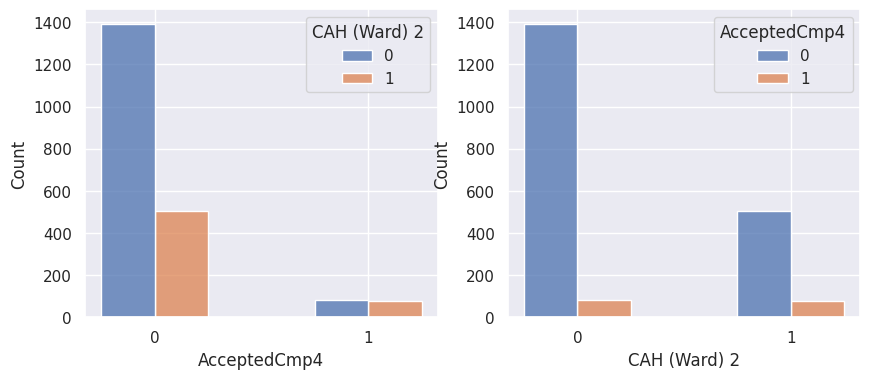
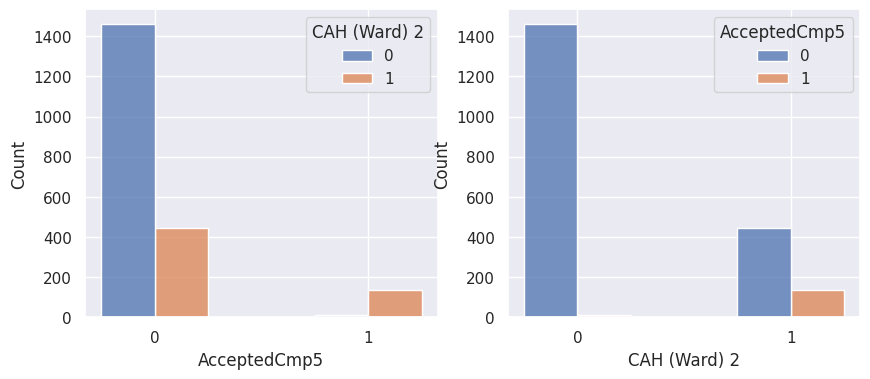
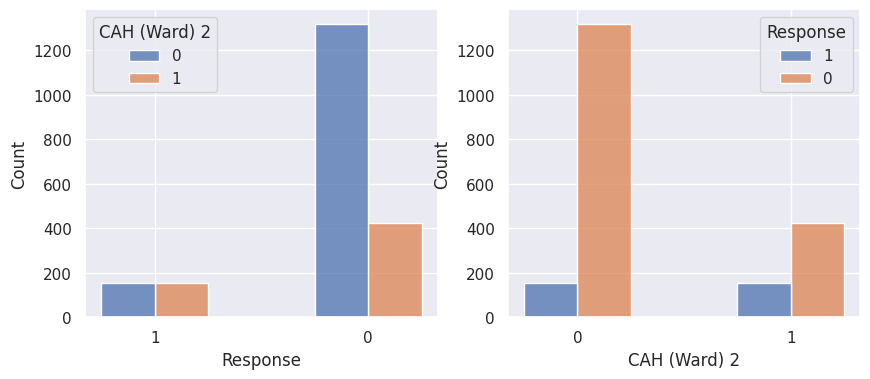
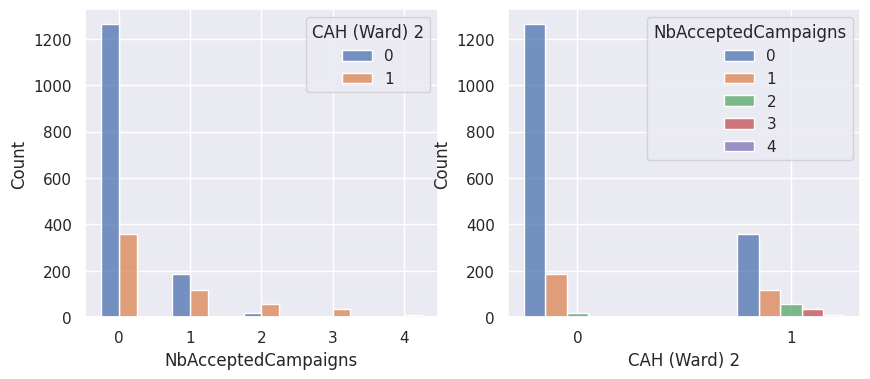
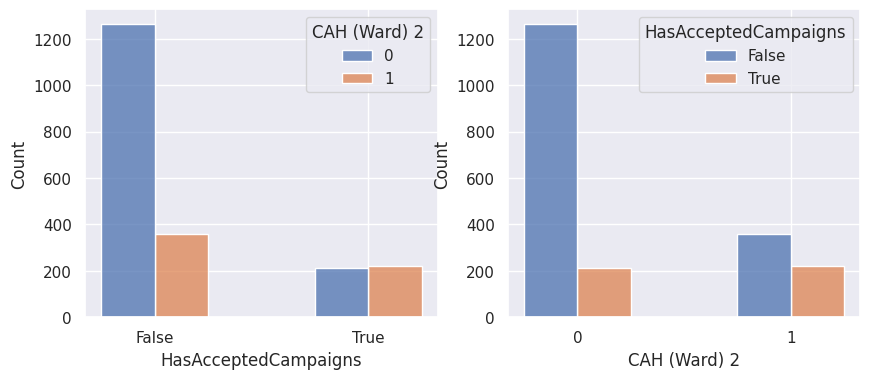
affiche_clusters("CAH (Ward) 2")

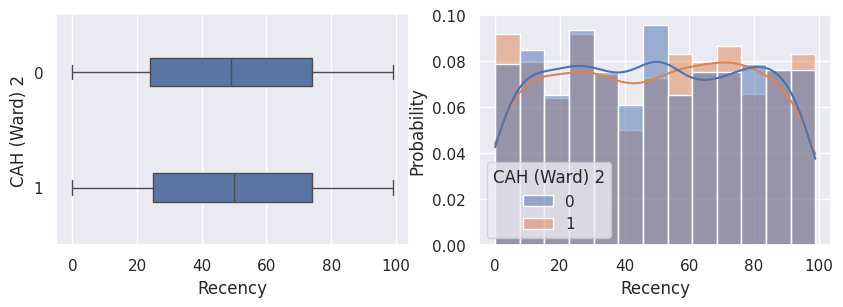
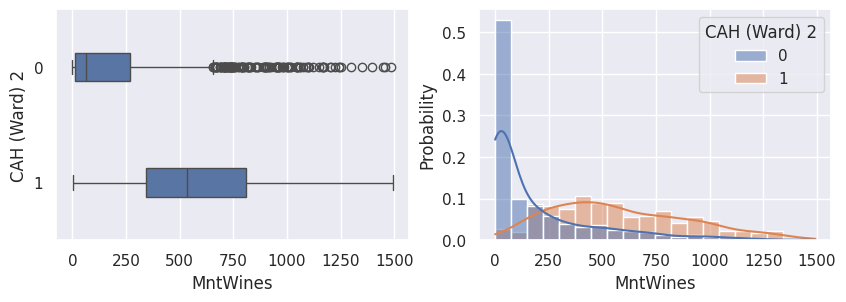
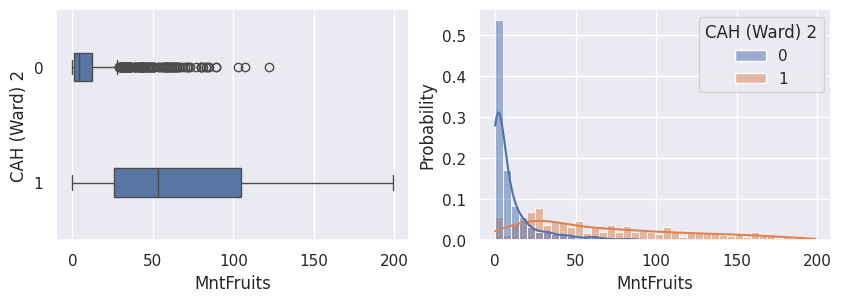
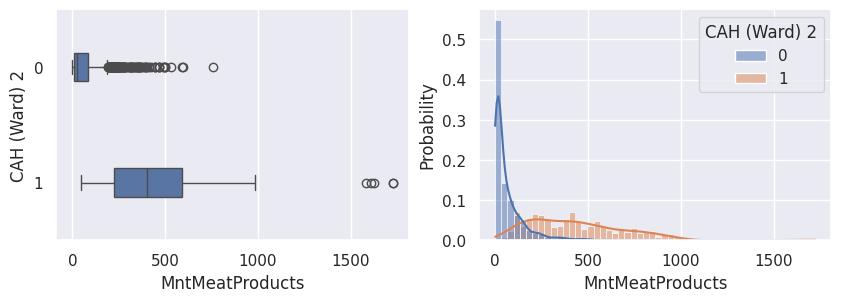
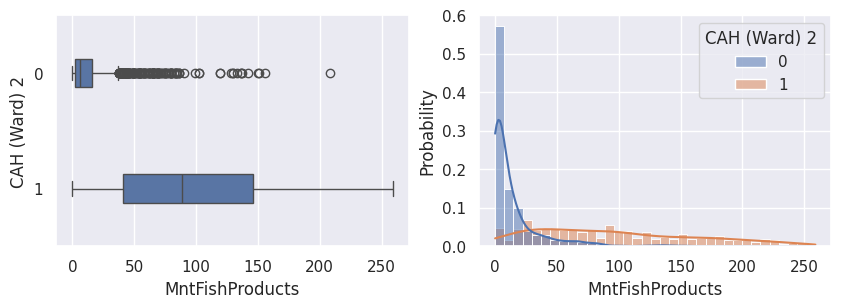
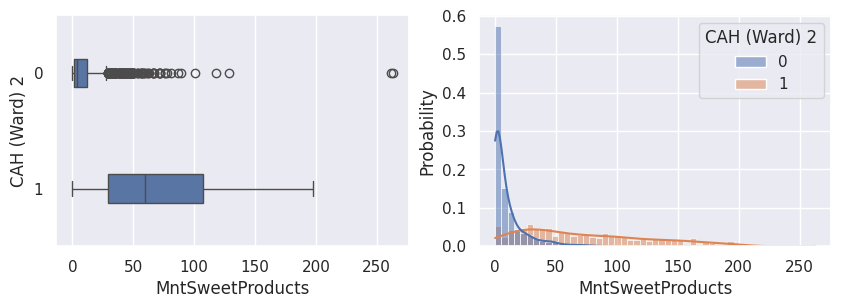
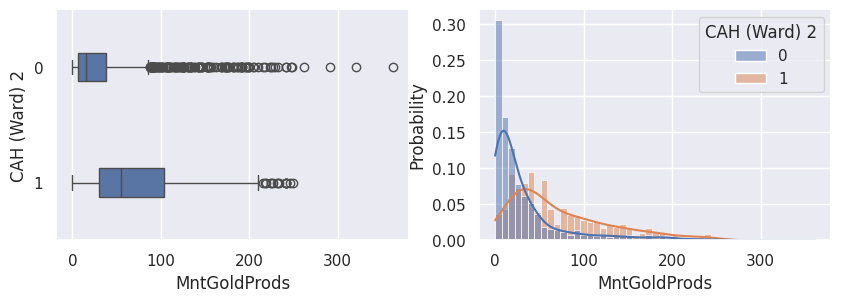
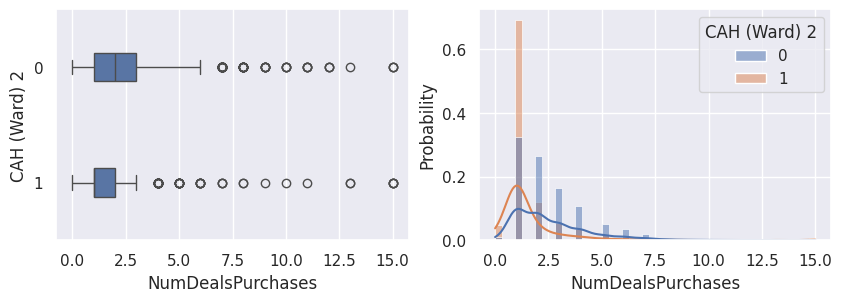
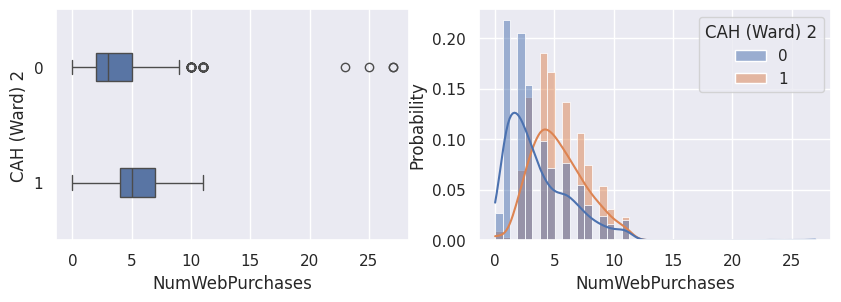
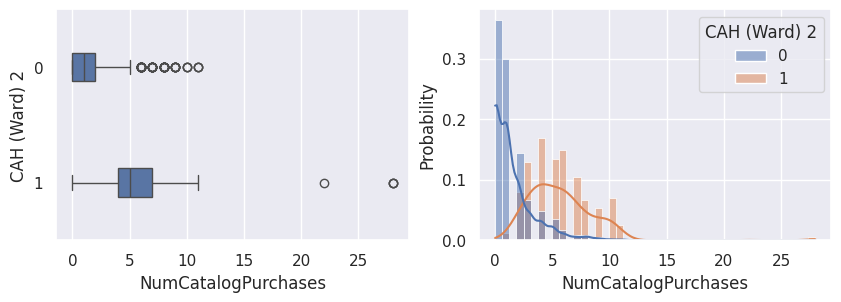
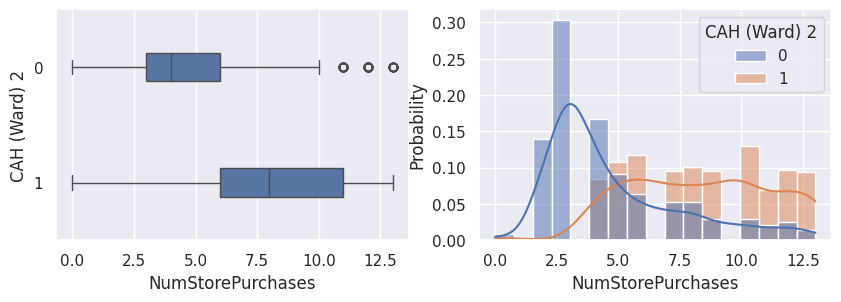
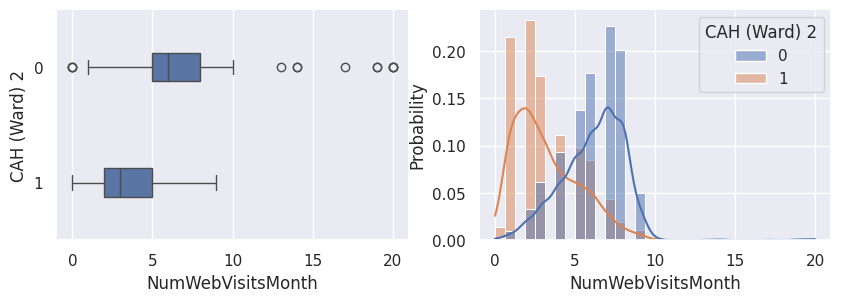
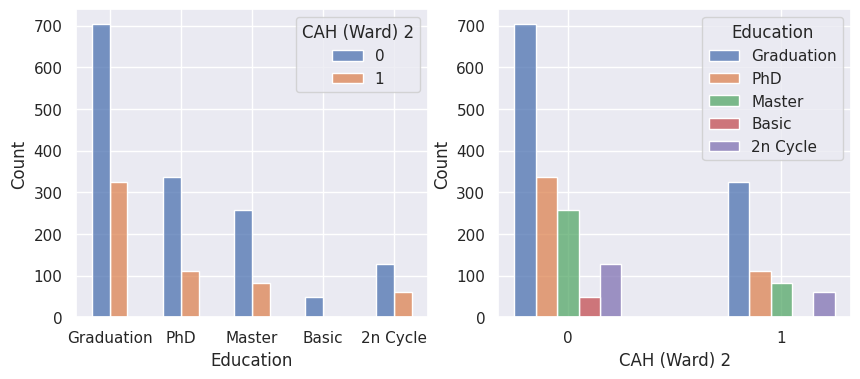
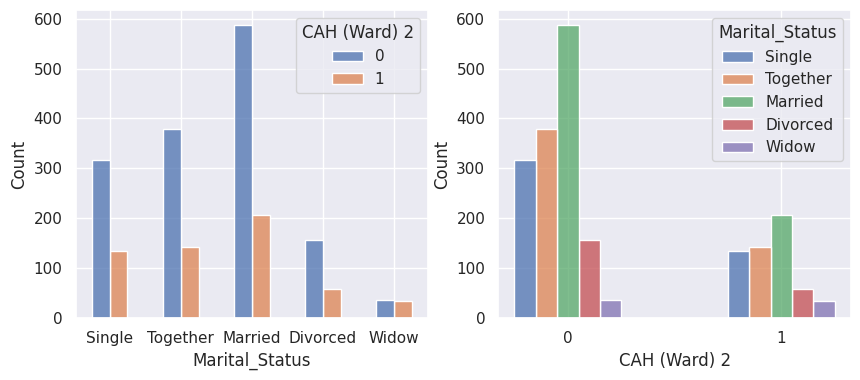
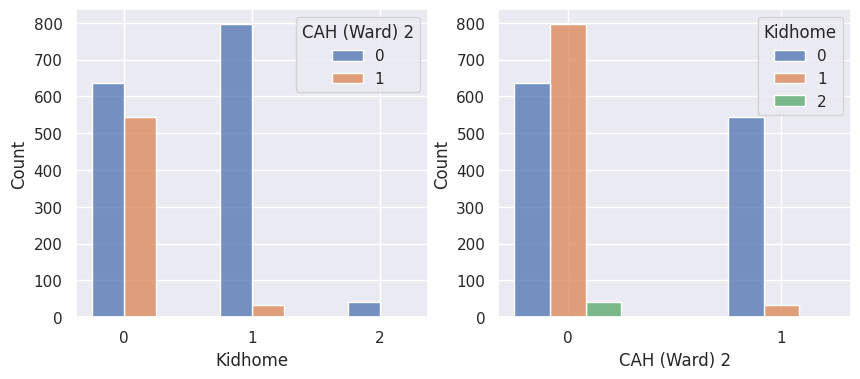
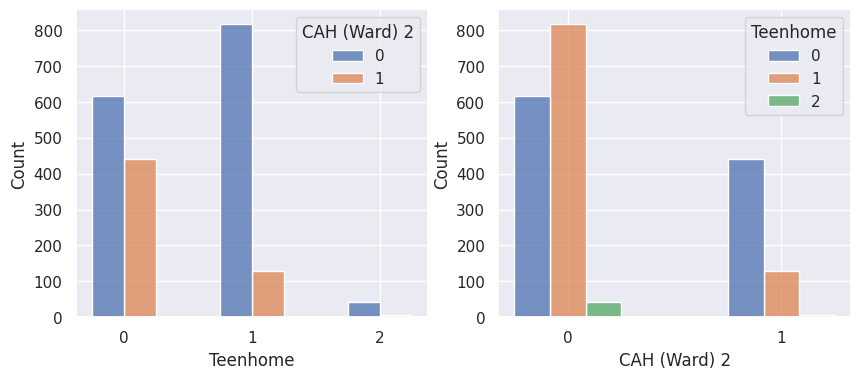
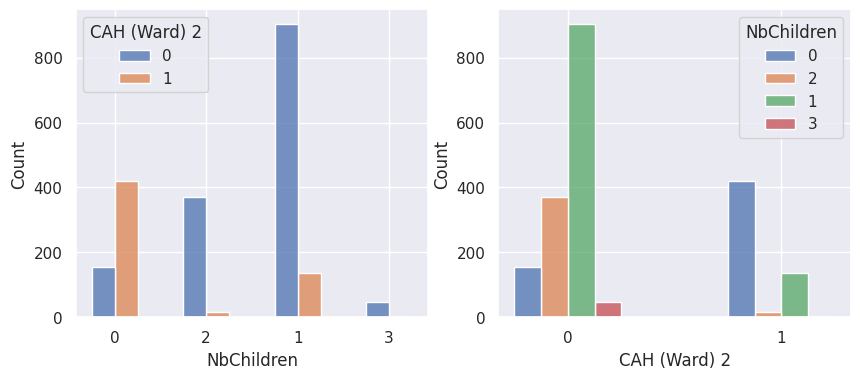
Conclusion

Tableau. Description des clients types

Profil	Proportion	Education	Revenu	Campagnes acceptées	Enfants	Dépenses	Année de naissance	Site Internet
Clients qui achètent	30%	Bac - doctorat	Élevé	0-4	0 bas-âge 0-1 ado	Élevées	1970	Peu de visites
Clients qui n’achètent pas ou peu	68% - 70%	Brevet - doctorat	Moyen	0-1	0-3 enfants (bas-âge et ado)	Peu élevées	1970	Beaucoup de visites
Clients qui n’achètent pas (n=3)	2%	Brevet	Le plus faible	0	0-1 bas-âge 0 ado	Aucune	1980	Beaucoup de visites

Notons aussi que parmi les clients qui achètent, la proportion d’acceptation des campagnes est beaucoup plus élevée.

Pour aller plus loin

• tester la stabilité des clusters (ici, l’initialisation des algorithmes a un impact significatif sur les clusters trouvés)

• tester les différents paramètres de chacun des algorithmes de clusters pour comparaison

• tester les algorithmes de clustering sur différents sous-ensembles de variables pour exhiber différents groupes

Sauvegarde des données

## todo: sauvegarder les clusters