Régression supervisée

Import des outils / jeu de données

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error, accuracy_score
from sklearn.model_selection import train_test_split

from src.utils import init_notebook
from sklearn.linear_model import LogisticRegression

init_notebook()

df = pd.read_csv(
    "data/kickstarter_1.csv",
    parse_dates=True,
)
event_times = df["day_succ"]
event_observed = df["Status"]

event_times_no_censoring = df["day_succ"][df["Status"] == 1]
event_observed_no_censoring = df["Status"][df["Status"] == 1]

On ne s’intéresse qu’aux variables suivantes

df = df[
    [
        "day_succ",
        "Status",
        "has_video",
        "facebook_connected",
        "goal",
        "facebook_friends",
    ]
]

Régression logistique

Nous cherchons à prévoir si le projet sera financé dans les 60 jours impartis ou non.

X = df.drop(["day_succ", "Status"], axis=1)
y = event_observed

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
y_pred = log_reg.predict(X_test)

accuracy = accuracy_score(y_test, y_pred)
accuracy

0.629940119760479

Nous obtenons une accuracy de 62%, ce qui est relativement peu.

# Get coefficients
log_reg_coeff = pd.DataFrame(
    {"Variable": [col for col in X.columns], "Coefficient": log_reg.coef_[0].tolist()}
)
log_reg_coeff

	Variable	Coefficient
0	has_video	0.848165
1	facebook_connected	-0.009586
2	goal	-6.582300
3	facebook_friends	0.366086

Régression linéaire

Nous cherchons à déterminer quelle est la durée de financement d’un projet, sachant qu’il a été financé.

# Redefine variables
X = df[event_observed == 1].drop(["Status", "day_succ"], axis=1)
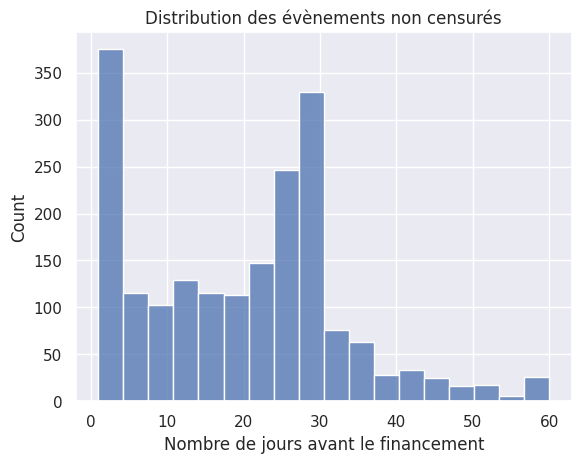
y = df["day_succ"][event_observed == 1]

sns.histplot(y)
plt.title("Distribution des évènements non censurés")
plt.xlabel("Nombre de jours avant le financement")

Text(0.5, 0, 'Nombre de jours avant le financement')

Modèle explicatif

# Add constant
X = sm.add_constant(X)

# Define and fit model
linear_explic = sm.OLS(y, X).fit()

# Predict
y_pred_explic = linear_explic.predict(X)

# Calculate residuals
residuals_explic = y_pred_explic - y

Diagnostic

linear_explic.summary()

OLS Regression Results

Dep. Variable:	day_succ	R-squared:	0.017
Model:	OLS	Adj. R-squared:	0.015
Method:	Least Squares	F-statistic:	8.626
Date:	Mon, 15 Jan 2024	Prob (F-statistic):	6.71e-07
Time:	23:44:53	Log-Likelihood:	-7852.4
No. Observations:	1962	AIC:	1.571e+04
Df Residuals:	1957	BIC:	1.574e+04
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	17.1439	1.006	17.048	0.000	15.172	19.116
has_video	2.5783	0.904	2.853	0.004	0.806	4.351
facebook_connected	1.2968	0.670	1.936	0.053	-0.017	2.610
goal	32.5965	10.546	3.091	0.002	11.914	53.279
facebook_friends	0.8303	0.311	2.670	0.008	0.220	1.440

Omnibus:	44.454	Durbin-Watson:	0.034
Prob(Omnibus):	0.000	Jarque-Bera (JB):	46.567
Skew:	0.367	Prob(JB):	7.73e-11
Kurtosis:	2.827	Cond. No.	56.2

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

• Un objectif financier (goal) ambitieux signifie plus de temps avant d’atteindre le financement. C’est la variable la plus influente.

• Avoir une vidéo pour promouvoir le projet est très favorable.

• Plus le compte facebook du projet a d’abonnés, plus la durée de financement est courte.

• facebook_connected engendre un problème de multicolinéarité avec facebook_friends et n’est donc pas significative. On la retire de l’analyse.

# Drop variable
X = X.drop("facebook_connected", axis=1)

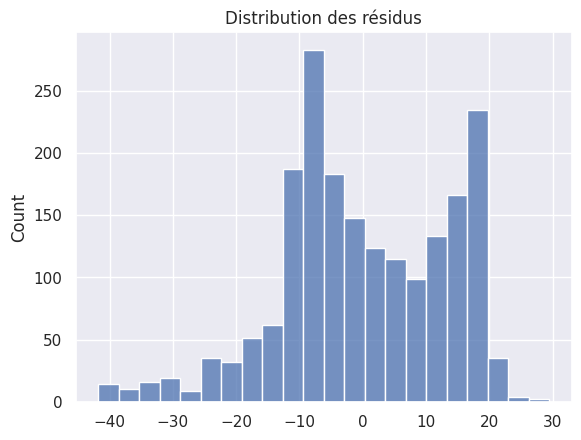
sns.histplot(residuals_explic)
plt.title("Distribution des résidus")

Text(0.5, 1.0, 'Distribution des résidus')

Modèle prédictif

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

linear = LinearRegression(fit_intercept=False)
linear.fit(X_train, y_train)

LinearRegression(fit_intercept=False)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Get coefficients
coefficients_df = pd.DataFrame(
    {"Variable": [col for col in X.columns], "Coefficient": linear.coef_.tolist()}
)
coefficients_df

	Variable	Coefficient
0	const	17.190159
1	has_video	3.026888
2	goal	19.910159
3	facebook_friends	1.212761

# Evaluate model prediction capacity
y_pred = linear.predict(X_test)

linear_mse = mean_squared_error(y_true=y_test, y_pred=y_pred)
linear_mae = mean_absolute_error(y_true=y_test, y_pred=y_pred)

print(f"Mean squared error = {round(linear_mse)}")
print(f"Mean absolute error = {round(linear_mae)}")

Mean squared error = 188
Mean absolute error = 12

En moyenne, le modèle de régression linéaire parvient à prévoir la durée nécessaire au financement à 12 jours près.

Forêt aléatoire

# Create and train a Random Forest Regressor
random_forest = RandomForestRegressor(n_estimators=100, random_state=42)
random_forest.fit(X_train, y_train)

RandomForestRegressor(random_state=42)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Get feature importances
feature_importances = random_forest.feature_importances_

# Display feature importances
importances_df = pd.DataFrame(
    {"Variable": [col for col in X.columns], "Importance": feature_importances.tolist()}
)
importances_df

	Variable	Importance
0	const	0.000000
1	has_video	0.033123
2	goal	0.415424
3	facebook_friends	0.551453

# Evaluate model prediction capacity
y_pred_rf = random_forest.predict(X_test)

# Calculate Mean Squared Error and Mean Absolute Error
rf_mse = mean_squared_error(y_true=y_test, y_pred=y_pred_rf)
rf_mae = mean_absolute_error(y_true=y_test, y_pred=y_pred_rf)

print(f"Random Forest Mean Squared Error = {round(rf_mse)}")
print(f"Random Forest Mean Absolute Error = {round(rf_mae)}")

Random Forest Mean Squared Error = 211
Random Forest Mean Absolute Error = 11

En moyenne, le modèle de forêt aléatoire parvient à prévoir la durée nécessaire au financement à 11 jours près.

Réseau de neurones

from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error

# Create and train a Multi-layer Perceptron Regressor
mlp_regressor = MLPRegressor(hidden_layer_sizes=(64, 32), max_iter=1000, random_state=42)
mlp_regressor.fit(X_train, y_train)

# Evaluate model prediction capacity
y_pred_mlp = mlp_regressor.predict(X_test)

# Calculate Mean Squared Error and Mean Absolute Error
mlp_mse = mean_squared_error(y_true=y_test, y_pred=y_pred_mlp)
mlp_mae = mean_absolute_error(y_true=y_test, y_pred=y_pred_mlp)

print(f"MLP Regressor Mean Squared Error = {round(mlp_mse)}")
print(f"MLP Regressor Mean Absolute Error = {round(mlp_mae)}")

MLP Regressor Mean Squared Error = 190
MLP Regressor Mean Absolute Error = 12

En moyenne, le réseau de neurones parvient à prévoir la durée nécessaire au financement à 12 jours près.

---

Bilan

Régression logistique	Accuracy
Le projet sera-t-il financé ?	62%

Tableau. Modèle de prévision et MAE correspondante obtenue sur l’ensemble de test

Modèle	MAE
Régression Linéaire	12 jours
Forêt Aléatoire	11 jours
Réseau de Neurones	12 jours

On conservera donc le modèle de forêt aléatoire pour la prédiction.