Estimation non-paramétrique univariée

Objectif

• modéliser les fonctions de survie et de risque avec Kaplan-Meier & Nelson-Aalen

• étudier l’impact de la censure sur les estimateurs

• étudier l’impact d’une vidéo promotionnelle sur les estimateurs

Import des outils / jeu de données

import pandas as pd

from src.modelisation.univariate.non_parametric.models import (
    create_hazard_models,
    create_survival_models,
)
from src.modelisation.univariate.parametric.plot import (
    plot_hazard_estimation,
    plot_survival_estimation,
)
from src.utils import init_notebook

init_notebook()

Données

df = pd.read_csv(
    "data/kickstarter_1.csv",
    parse_dates=True,
)

event_times = df["day_succ"]
event_observed = df["Status"]

event_times_no_censoring = df["day_succ"][df["Status"] == 1]
event_observed_no_censoring = df["Status"][df["Status"] == 1]

df_video = df[df["has_video"] == 1].copy()
df_no_video = df[df["has_video"] == 0].copy()

t_video = df_video["day_succ"]
o_video = df_video["Status"]

t_no_video = df_no_video["day_succ"]
o_no_video = df_no_video["Status"]

Fonction de survie

survival_models = create_survival_models()

Kaplan-Meier

Formalisation du problème

Soit \(\tau\) une variable aléatoire à valeur dans \(\mathbb{N}^*\) modélisant le jour de succès d’un projet Kickstarter.
On se munit d’un échantillon \(\tau_1,\dots,\tau_n\) de variables aléatoires indépendantes identiquement distribuées suivant la même loi que \(\tau\) et de \((c_1, \dots, c_n)\) le vecteur déterministe des instants de censure tel que

\[\begin{split} c_j = \begin{cases} t & \text{si l'évènement } j \text{ est censuré au jour } t\in \mathbb{N}\\ + \infty & \text{sinon} \end{cases} \hspace{12px} \forall j \in [1 ; n] \end{split}\]

Pour construire l’estimateur de Kaplan-Meier et afin de prendre en compte la censure, on s’intéresse aux couples d’observations \(( \tilde \tau_j, c_j )_{j=1,\dots,n}\)
où \(\tilde \tau_j = \min(\tau_j,c_j)\) pour tout \(j \in [1 ; n]\).

Calcul de l’estimateur de Kaplan-Meier

Fonction du survie

Soit un jour \(t \in \mathbb{N}\), la fonction du survie pour \(t\) vaut :

\[\begin{split}\begin{align} S(t) & = \operatorname{Prob}(\tau > t ) \hspace{12px} \text{par définition} \\[4pt] & = \operatorname{Prob}(\tau > t\mid\tau > t-1)\operatorname{Prob}(\tau > t-1) \\[4pt] & = (1-\operatorname{Prob}(\tau\le t\mid\tau > t-1)) \operatorname{Prob}(\tau > t-1)\\[4pt] & = (1-\operatorname{Prob}(\tau=t\mid\tau \ge t)) \operatorname{Prob}(\tau > t-1) \\[4pt] & = q(t) S(t-1)\,, \end{align}\end{split}\]

où \(q(t) = 1-\operatorname{Prob}(\tau=t\mid\tau\ge t)\).

Par itération on obtient $\( S(t) = q(t) q(t-1) \cdots q(0). \)$

Construction d’un estimateur de \(q(t)\)

Soit \(t \in \mathbb{N}\)

\[\begin{split} \begin{align} q(t) & = 1-\operatorname{Prob}(\tau=t\mid\tau\ge t) \\ & = 1 - \frac{\operatorname{Prob}(\tau=t, \tau \ge t)}{\operatorname{Prob}(\tau \ge t)} \hspace{12px} \text{d'après la définition de la probabilité conditionnelle} \\ & = 1 - \frac{\operatorname{Prob}(\tau=t)}{\operatorname{Prob}(\tau \ge t)} \end{align} \end{split}\]

De plus, on a les égalités suivantes : $\( \operatorname{Prob}(\tau=s) = \operatorname{Prob}(\tilde \tau_k=s) \)\( \)\( \operatorname{Prob}(\tau\ge s) = \operatorname{Prob}(\tilde \tau_k\ge s) \)$

Un estimateur de \(q(t)\) est alors donné par :

\[\begin{split} \begin{align} \hat q(t) & = 1 - \frac{|\{1\le k\le n\,:\, c_k\ge t,\tilde \tau_k=t\}|}{|\{1\le k \le n\,:\, c_k\ge t, \tilde \tau_k\ge t\}|} \\ & = 1 - \frac{|\{1\le k\le n\,:\,\tilde \tau_k=t\}|}{|\{1\le k \le n\,:\, \tilde \tau_k\ge t\}|} \hspace{12px} \text{ car $c_k \ge \tilde \tau_k = \min(\tau_k,c_k)$ } \\ & = \frac{d(t)}{n(t)} \end{align} \end{split}\]

où \(d(t)\) est le nombre de succès connus au temps \(t\)
et \(n(t)\) est le nombre de projets qui n’ont pas encore réussi et non censurés au temps \(t-1\).

Retour au calcul de l’estimateur de Kaplan-Meier

Enfin, on a l’estimateur de Kaplan-Meier pour la fonction de survie avec la censure : $\( \hat S(t) = \prod_{i:t_i\le t} \left(1-\frac{d_i}{n_i}\right) \)$

Propriétés statistiques de l’estimateur de Kaplan-Meier

Biais

• Estimateur à biais positif : \(bias[\hat S(t)] = \mathbb{E}[\hat S(t)]- S(t) >= 0\)

• Estimateur asymptotiquement sans biais : \(\displaystyle \lim_{n \to +\infty} \hat S(t) = 0\)

Variance

Une façon courante de calculer la variance est la formule de Greenwood : $\( \widehat{\operatorname{Var}} \left( \widehat S(t) \right) = \widehat S(t)^2 \sum_{i:\ t_i\le t} \frac{d_i}{n_i(n_i-d_i)} \hspace{12px} \forall t \in \mathbb{N} \)$

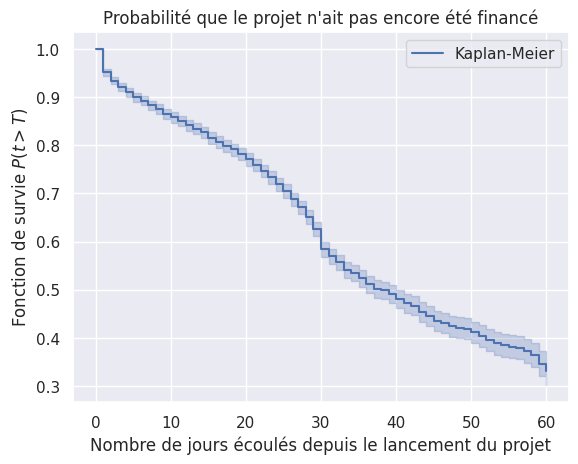
plot_survival_estimation(
    survival_models["Kaplan-Meier"], event_times, event_observed, "Kaplan-Meier"
)

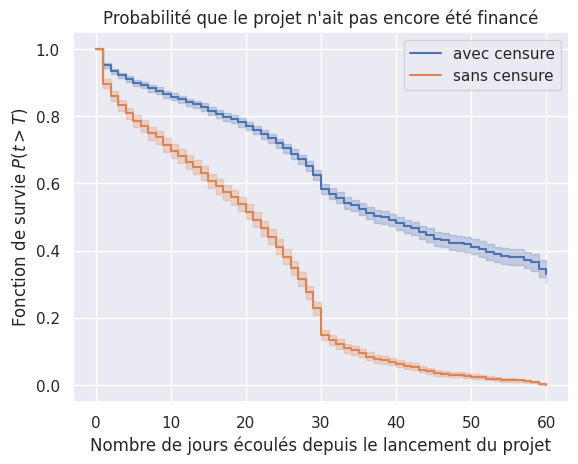
Kaplan-Meier (avec et sans censure)

plot_survival_estimation(
    survival_models["Kaplan-Meier"], event_times, event_observed, "avec censure"
)
plot_survival_estimation(
    survival_models["Kaplan-Meier"],
    event_times_no_censoring,
    event_observed_no_censoring,
    "sans censure",
)

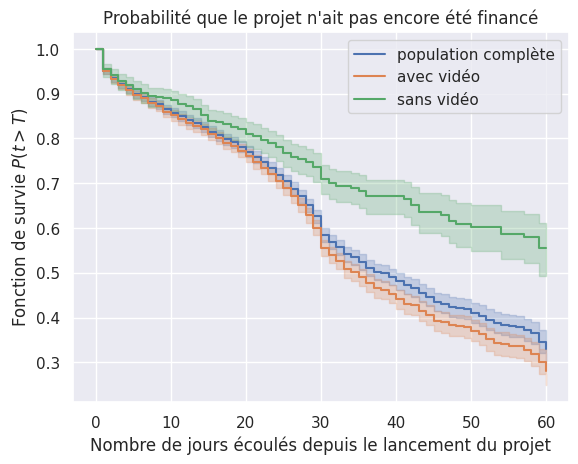
Co-variables

Vidéo de présentation

plot_survival_estimation(
    survival_models["Kaplan-Meier"], event_times, event_observed, "population complète"
)
plot_survival_estimation(
    survival_models["Kaplan-Meier"], t_video, o_video, "avec vidéo"
)
plot_survival_estimation(
    survival_models["Kaplan-Meier"], t_no_video, o_no_video, "sans vidéo"
)

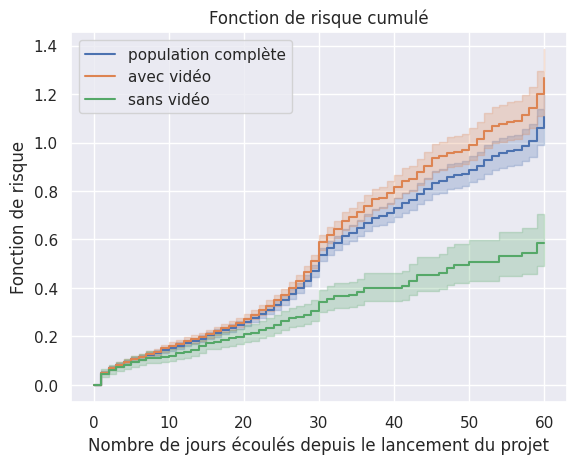
Fonction de risque

hazard_models = create_hazard_models()

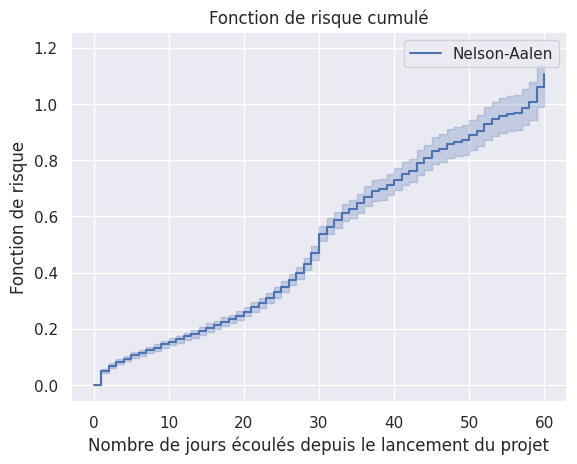
Nelson-Aalen

plot_hazard_estimation(
    hazard_models["Nelson-Aalen"], event_times, event_observed, "Nelson-Aalen"
)

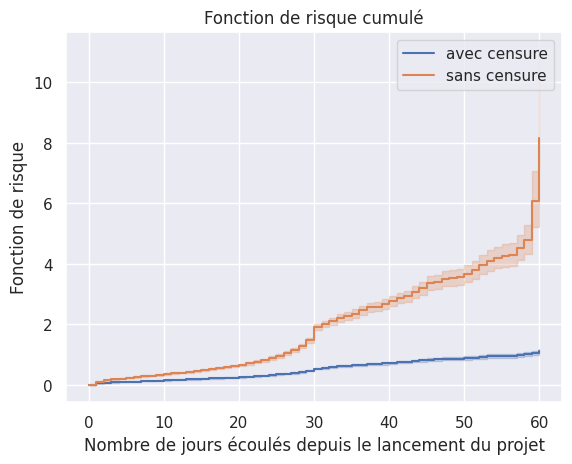
Nelson-Aalen (avec et sans censure)

plot_hazard_estimation(
    hazard_models["Nelson-Aalen"], event_times, event_observed, "avec censure"
)
plot_hazard_estimation(
    hazard_models["Nelson-Aalen"],
    event_times_no_censoring,
    event_observed_no_censoring,
    "sans censure",
)

Co-variables

Vidéo de présentation

plot_hazard_estimation(
    hazard_models["Nelson-Aalen"], event_times, event_observed, "population complète"
)
plot_hazard_estimation(hazard_models["Nelson-Aalen"], t_video, o_video, "avec vidéo")
plot_hazard_estimation(
    hazard_models["Nelson-Aalen"], t_no_video, o_no_video, "sans vidéo"
)