Estimation paramétrique univariée#
Objectif
modéliser les fonctions de survie et de risque avec des modèles paramétriques
choisir le meilleur modèle paramétrique
étudier l’impact d’une vidéo promotionnelle d’après notre meilleur estimateur
Import des outils / jeu de données#
1import numpy as np
2import pandas as pd
3import seaborn as sns
4from lifelines import (
5 ExponentialFitter,
6 GeneralizedGammaFitter,
7 LogLogisticFitter,
8 LogNormalFitter,
9 PiecewiseExponentialFitter,
10 WeibullFitter,
11)
12from lifelines.plotting import qq_plot
13from lifelines.utils import find_best_parametric_model
14from matplotlib import pyplot as plt
15from scipy import stats
16from scipy.stats import kstest
17
18from src.modelisation.univariate.non_parametric.models import (
19 create_hazard_models,
20 create_survival_models,
21)
22from src.modelisation.univariate.parametric.models import create_models
23from src.modelisation.univariate.parametric.plot import (
24 plot_hazard_estimation,
25 plot_hazard_estimations,
26 plot_survival_estimation,
27 plot_survival_estimations,
28)
29from src.utils import init_notebook
1init_notebook()
1df = pd.read_csv(
2 "data/kickstarter_1.csv",
3 parse_dates=True,
4)
1event_times = df["day_succ"]
2event_observed = df["Status"]
3
4event_times_no_censoring = df["day_succ"][df["Status"] == 1]
5event_observed_no_censoring = df["Status"][df["Status"] == 1]
6df_video = df[df["has_video"] == 1].copy()
7df_no_video = df[df["has_video"] == 0].copy()
8
9t_video = df_video["day_succ"]
10o_video = df_video["Status"]
11
12t_no_video = df_no_video["day_succ"]
13o_no_video = df_no_video["Status"]
1models = create_models()
Modèles paramétriques testés#
1tableau = {
2 "Modèles paramétriques testées": [
3 """- Weibull
4- Exponentiel
5- Exponentiel par morceaux
6- Log-normal
7- Log-logistique
8- Gamma généralisé"""
9 ],
10 "**Critère de sélection**": [
11 """- test de Kolmogorov-Smirnov
12- QQ Plots
13- AIC
14- BIC"""
15 ],
16}
1# print(pd.DataFrame(tableau).to_markdown(index=False))
Tableau. Notre démarche pour les modèles paramétriques.
Modèles paramétriques testés |
Critère de sélection |
|---|---|
- Weibull |
- test de Kolmogorov-Smirnov |
- Exponentiel |
- QQ Plots |
- Exponentiel par morceaux |
- AIC |
- Log-normal |
- BIC |
- Log-logistique |
|
- Gamma généralisé |
Tests statistiques sur les distributions#
Histogrammes#
1_, axs = plt.subplots(1, 2, figsize=(12, 6))
2
3sns.histplot(event_times, ax=axs[0], bins=60)
4axs[0].set_title("Histogramme des durées de succès")
5axs[0].set_xlabel("Nombre de jours avant le succès du projet")
6
7sns.histplot(event_times_no_censoring, ax=axs[1], bins=60)
8axs[1].set_title("Histogramme des durées de succès non censurées")
9axs[1].set_xlabel("Nombre de jours avant le succès du projet")
Text(0.5, 0, 'Nombre de jours avant le succès du projet')
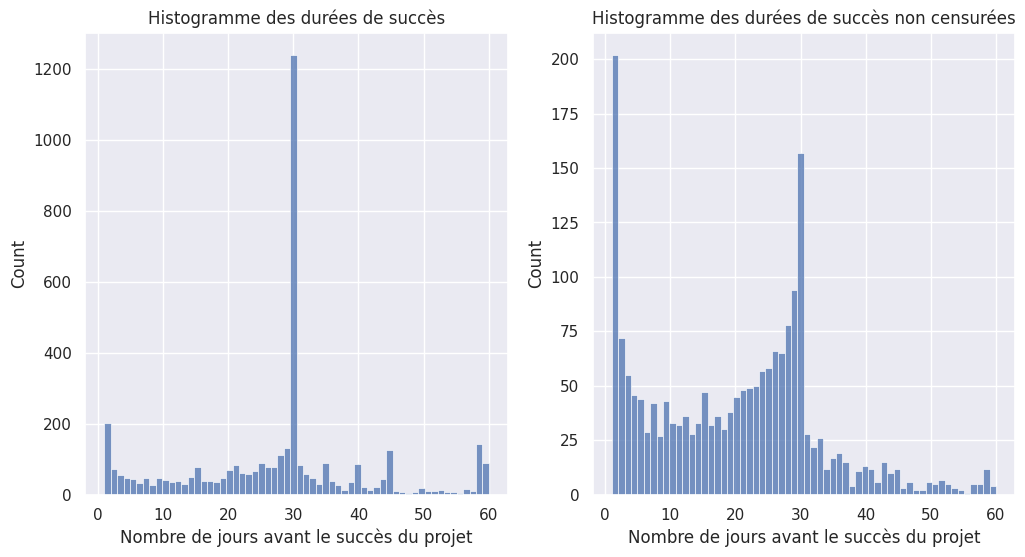
A première vue, la variable aléatoire de la durée s’écoulant avant le succès du projet ne suit pas une loi particulière.
Tests#
Le test bilatéral de Kolmogorov-Smirnov, implémenté dans scipy, teste les hypothèse suivantes:
\(H_0: F(t) = G(t), \hspace{10px} \forall t\)
\(H_1: F(t) \neq G(t), \hspace{10px} \forall t\)
1print(f"{best_model.lambda_0_ =}")
2print(f"{best_model.lambda_1_ =}")
3print(f"{best_model.lambda_2_ =}")
4print(f"{best_model.lambda_3_ =}")
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[9], line 1
----> 1 print(f"{best_model.lambda_0_ =}")
2 print(f"{best_model.lambda_1_ =}")
3 print(f"{best_model.lambda_2_ =}")
NameError: name 'best_model' is not defined
1breaks = [9.0, 21.0, 29.0]
1event_times_segments = [
2 event_times[event_times < breaks[0]],
3 event_times[(event_times >= breaks[0]) & (event_times < breaks[1])],
4 event_times[(event_times >= breaks[1]) & (event_times < breaks[2])],
5 event_times[event_times >= breaks[2]],
6]
1lambdas = [
2 best_model.lambda_0_,
3 best_model.lambda_1_,
4 best_model.lambda_2_,
5 best_model.lambda_3_,
6]
7ks_exp, p_value_exp = {}, {}
8
9for i, lambda_ in enumerate(lambdas):
10 ks_exp[f"segment_{i}"], p_value_exp[f"segment_{i}"] = kstest(
11 rvs=event_times_segments[i], # Random variable to test
12 cdf=stats.expon.cdf, # Reference CDF
13 args=(0, lambda_), # Reference distribution parameters
14 )
1print(f"Segmented exponential distribution p-values:")
2p_value_exp
Segmented exponential distribution p-values:
{'segment_0': 0.0,
'segment_1': 0.0,
'segment_2': 9.230707262794722e-168,
'segment_3': 0.0}
1mean = np.mean(event_times)
2std = np.std(event_times)
3
4ks_norm, p_value_norm = kstest(
5 rvs=event_times, # Random variable to test
6 cdf=stats.norm.cdf, # Reference CDF
7 args=(mean, std), # Reference distribution parameters
8)
9
10print(f"Gaussian distribution p-value = {p_value_norm}")
Gaussian distribution p-value = 7.382711171697777e-103
1ks_weibull, p_value_weibull = kstest(
2 rvs=event_times, # Random variable to test
3 cdf=stats.weibull_min.cdf, # Reference CDF
4 args=(1.5,), # Reference distribution parameters
5)
6
7print(f"Weibull distribution p-value = {p_value_weibull}")
Weibull distribution p-value = 0.0
1log_mean = np.log(mean)
2log_std = np.log(std)
3
4ks_lognorm, p_value_lognorm = kstest(
5 rvs=event_times, # Random variable to test
6 cdf=stats.lognorm.cdf, # Reference CDF
7 args=(1,), # Reference distribution parameters
8)
9
10print(f"Log-normal distribution p-value = {p_value_lognorm}")
Log-normal distribution p-value = 0.0
1ks_gamma, p_value_gamma = kstest(
2 rvs=event_times, # Random variable to test
3 cdf=stats.gamma.cdf, # Reference CDF
4 args=(1,), # Reference distribution parameters
5)
6
7print(f"Gamma distribution p-value = {p_value_gamma}")
Gamma distribution p-value = 0.0
1p_value_dict = {
2 "Distribution testée": [
3 "Weibull",
4 "Exponentiel",
5 "Log-normale",
6 "Log-logistique",
7 "Gamma généralisée",
8 ],
9 "p-value": [0, 0, 0, 0, 0],
10}
1df_p_value = pd.DataFrame(p_value_dict)
1# print(df_p_value.to_markdown(index=False))
Tableau. Distributions testées et p-values obtenues.
Distribution testée |
p-value |
|---|---|
Weibull |
0 |
Exponentiel |
0 |
Log-normale |
0 |
Log-logistique |
0 |
Gamma généralisée |
0 |
Comme attendu, la fonction de survie ne suit pas une loi particulière.
Fonction de survie#
Modèles paramétriques#
1plot_survival_estimations(models, event_times, event_observed)
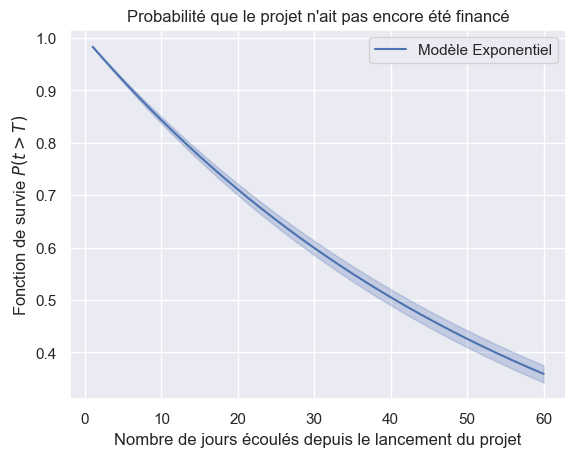
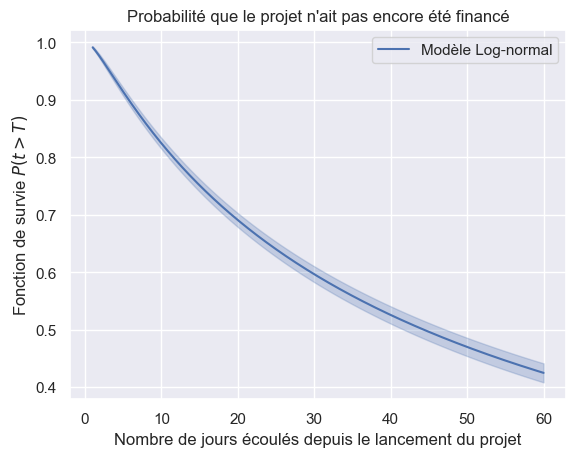
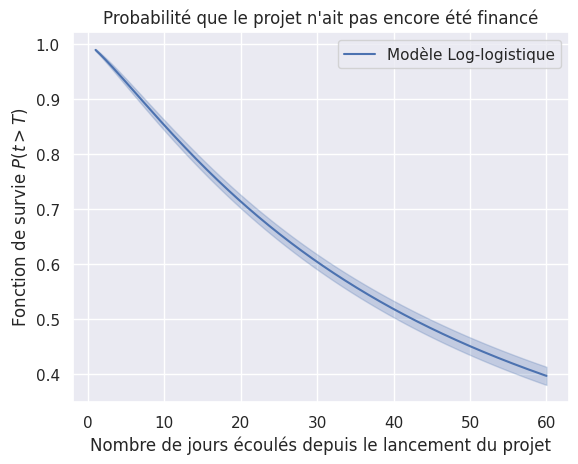
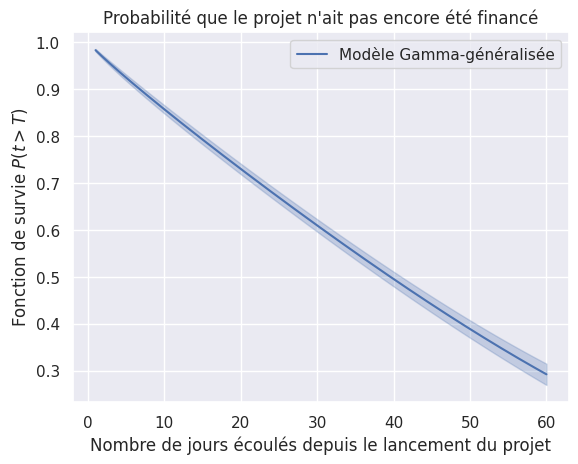
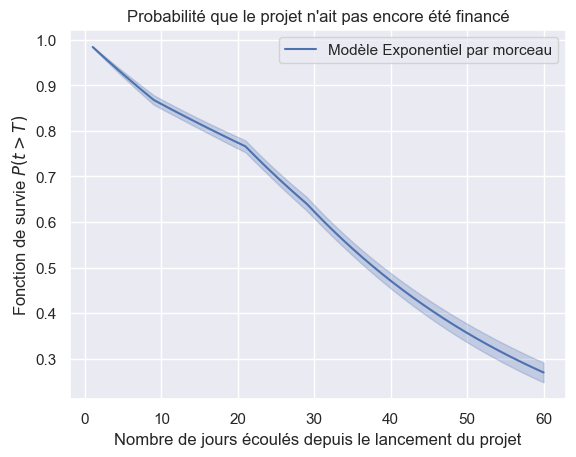
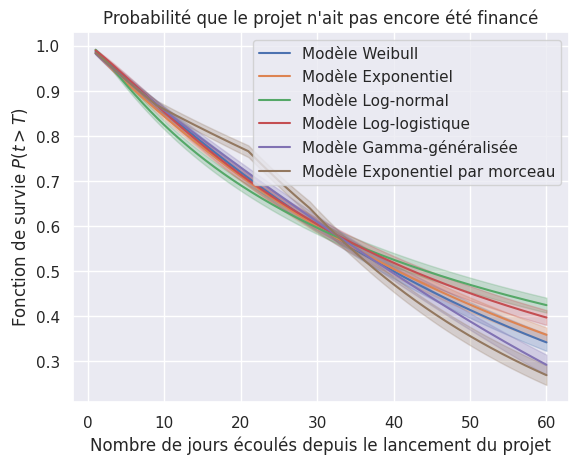
Toutes les fonctions de survie#
1# todo tracer kaplam meier et test de logrank
2plot_survival_estimations(models, event_times, event_observed, same_plot=True)
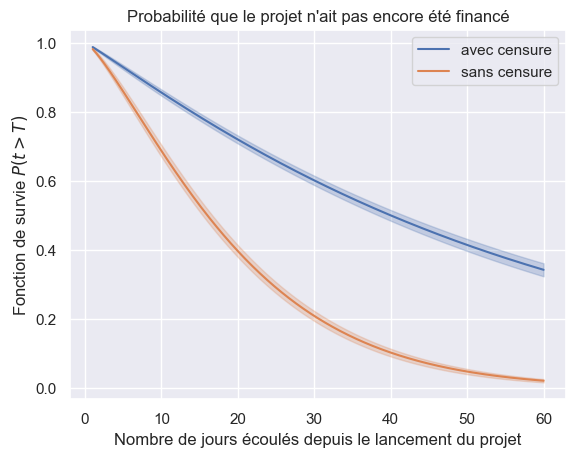
Impact de la censure#
1plot_survival_estimation(models["Weibull"], event_times, event_observed, "avec censure")
2plot_survival_estimation(
3 models["Weibull"],
4 event_times_no_censoring,
5 event_observed_no_censoring,
6 "sans censure",
7)
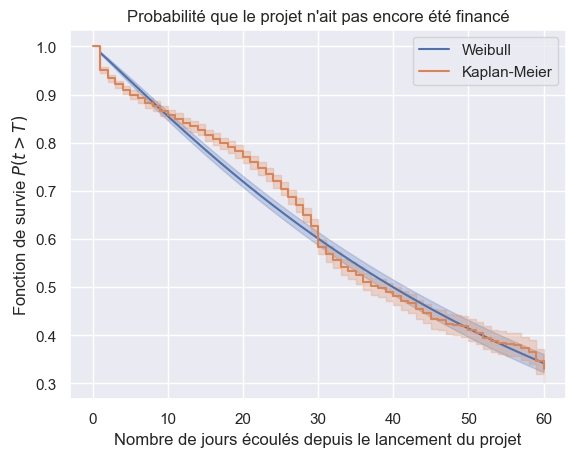
Comparaison avec modèles non-paramétriques#
1km = create_survival_models()["Kaplan-Meier"]
1plot_survival_estimation(models["Weibull"], event_times, event_observed, "Weibull")
2plot_survival_estimation(km, event_times, event_observed, "Kaplan-Meier")
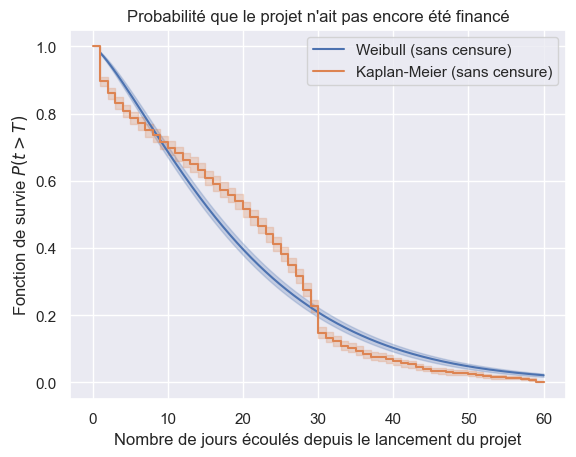
1plot_survival_estimation(
2 models["Weibull"],
3 event_times_no_censoring,
4 event_observed_no_censoring,
5 "Weibull (sans censure)",
6)
7plot_survival_estimation(
8 km,
9 event_times_no_censoring,
10 event_observed_no_censoring,
11 "Kaplan-Meier (sans censure)",
12)
Co-variables#
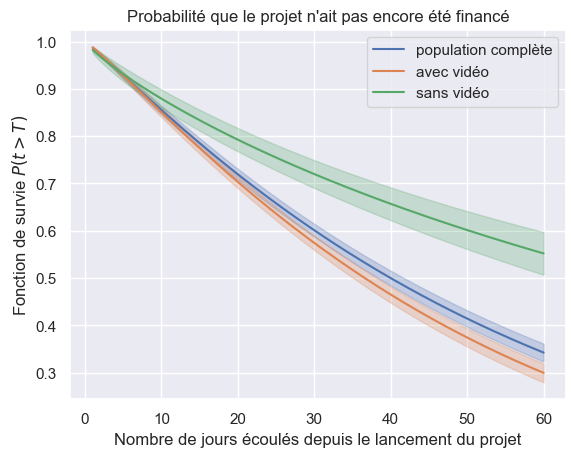
Vidéo de présentation#
1plot_survival_estimation(
2 models["Weibull"], event_times, event_observed, "population complète"
3)
4plot_survival_estimation(models["Weibull"], t_video, o_video, "avec vidéo")
5plot_survival_estimation(models["Weibull"], t_no_video, o_no_video, "sans vidéo")
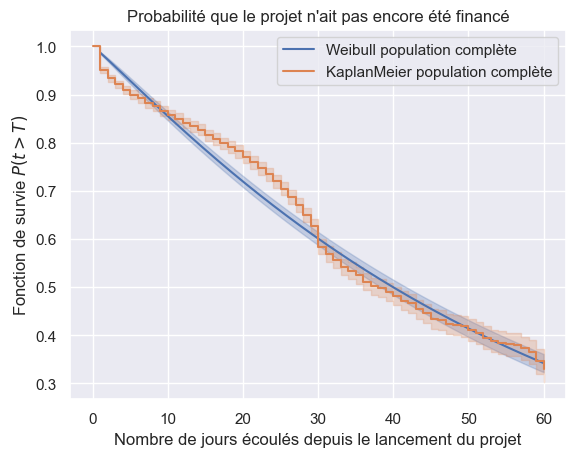
1for model in (models["Weibull"], km):
2 name = model.__class__.__name__.replace("Fitter", "")
3 plot_survival_estimation(
4 model, event_times, event_observed, f"{name} population complète"
5 )
6plt.show()
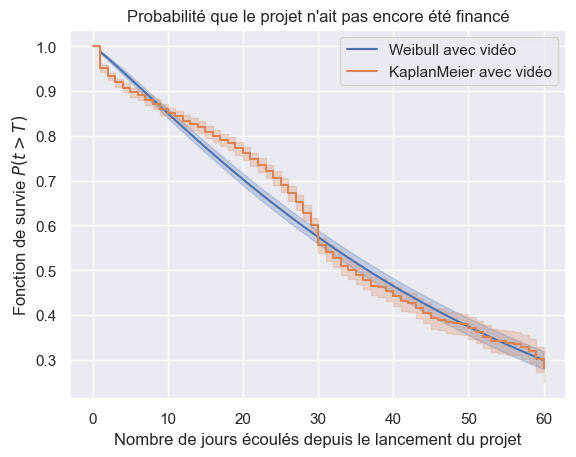
7for model in (models["Weibull"], km):
8 name = model.__class__.__name__.replace("Fitter", "")
9 plot_survival_estimation(model, t_video, o_video, f"{name} avec vidéo")
10
11plt.show()
12for model in (models["Weibull"], km):
13 name = model.__class__.__name__.replace("Fitter", "")
14 plot_survival_estimation(model, t_no_video, o_no_video, f"{name} sans vidéo")
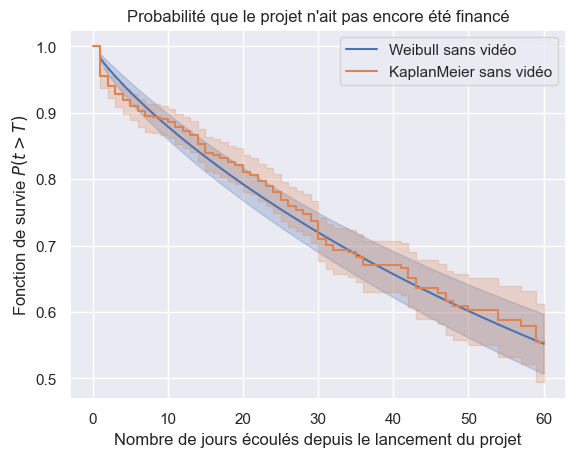
Fonction de risque#
1plot_hazard_estimations(models, event_times, event_observed)
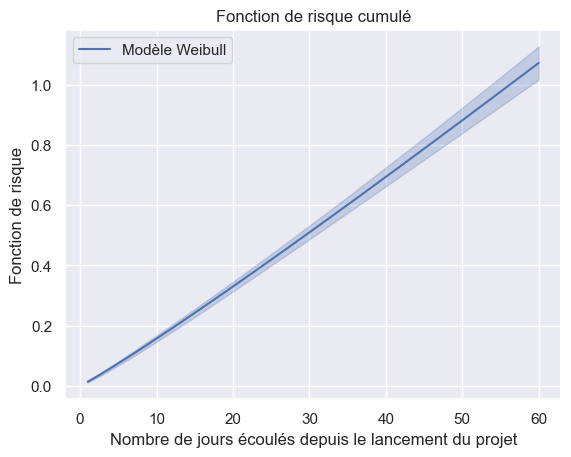
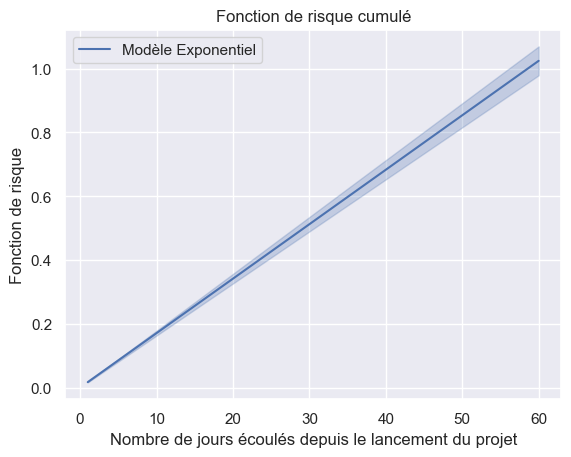
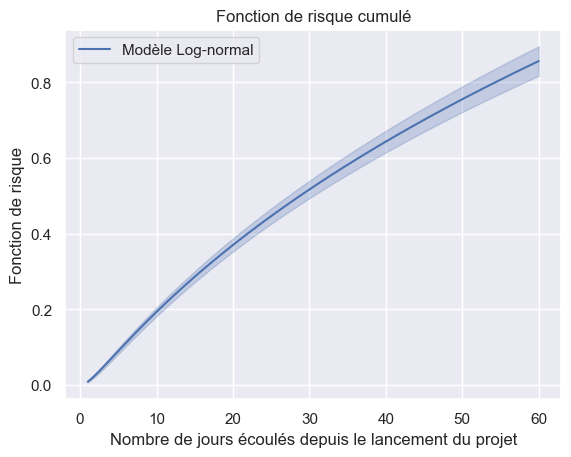
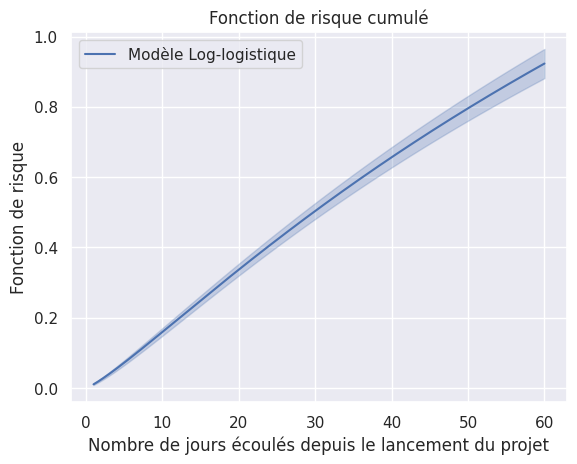
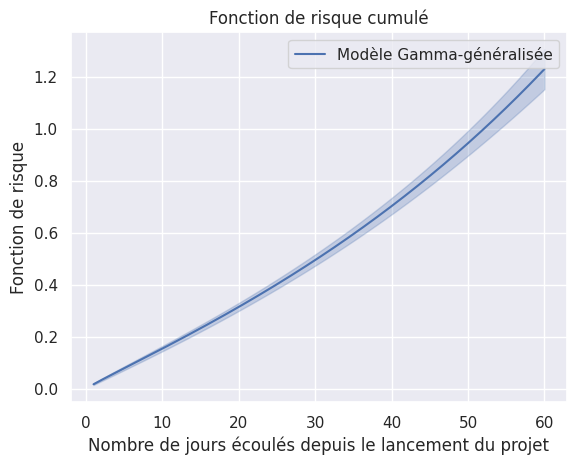
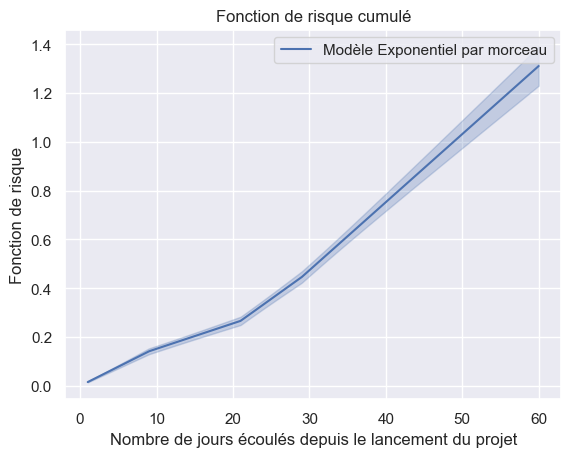
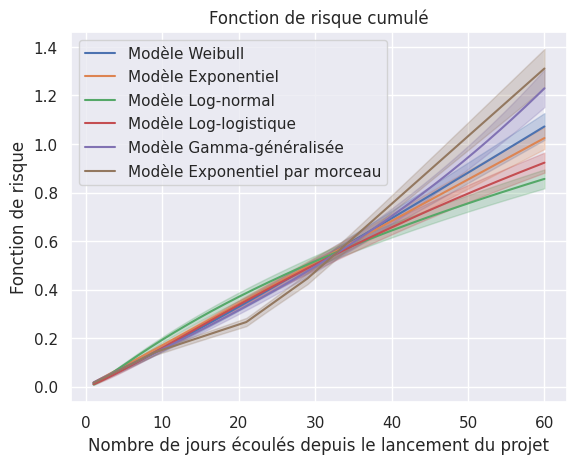
1plot_hazard_estimations(models, event_times, event_observed, same_plot=True)
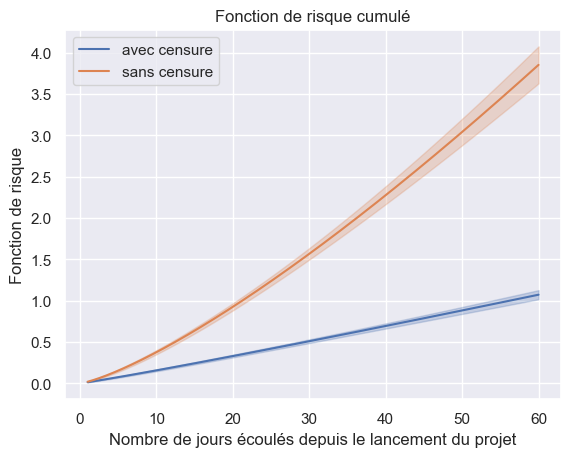
Impact de la censure#
1plot_hazard_estimation(models["Weibull"], event_times, event_observed, "avec censure")
2plot_hazard_estimation(
3 models["Weibull"],
4 event_times_no_censoring,
5 event_observed_no_censoring,
6 "sans censure",
7)
Co-variables#
Vidéo de présentation#
1plot_hazard_estimation(
2 models["Weibull"], event_times, event_observed, "population complète"
3)
4plot_hazard_estimation(models["Weibull"], t_video, o_video, "avec vidéo")
5plot_hazard_estimation(models["Weibull"], t_no_video, o_no_video, "sans vidéo")
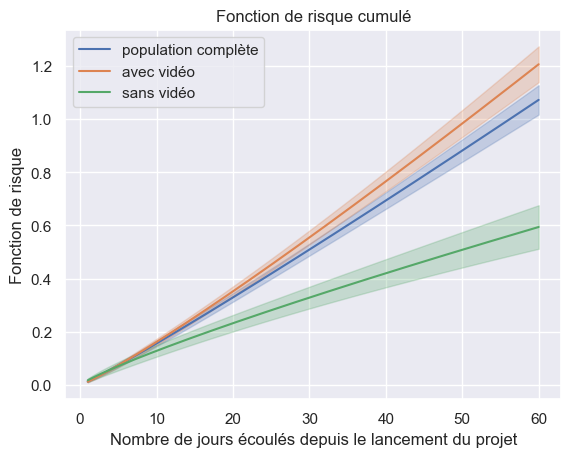
Comparaison de modèles paramétriques#
1best_model, best_aic_ = find_best_parametric_model(
2 event_times, event_observed, scoring_method="AIC"
3)
4
5print(best_model)
6
7best_model.plot_cumulative_hazard()
44.567842323678995
1best_model.breakpoints
array([ 9., 21., 29.])
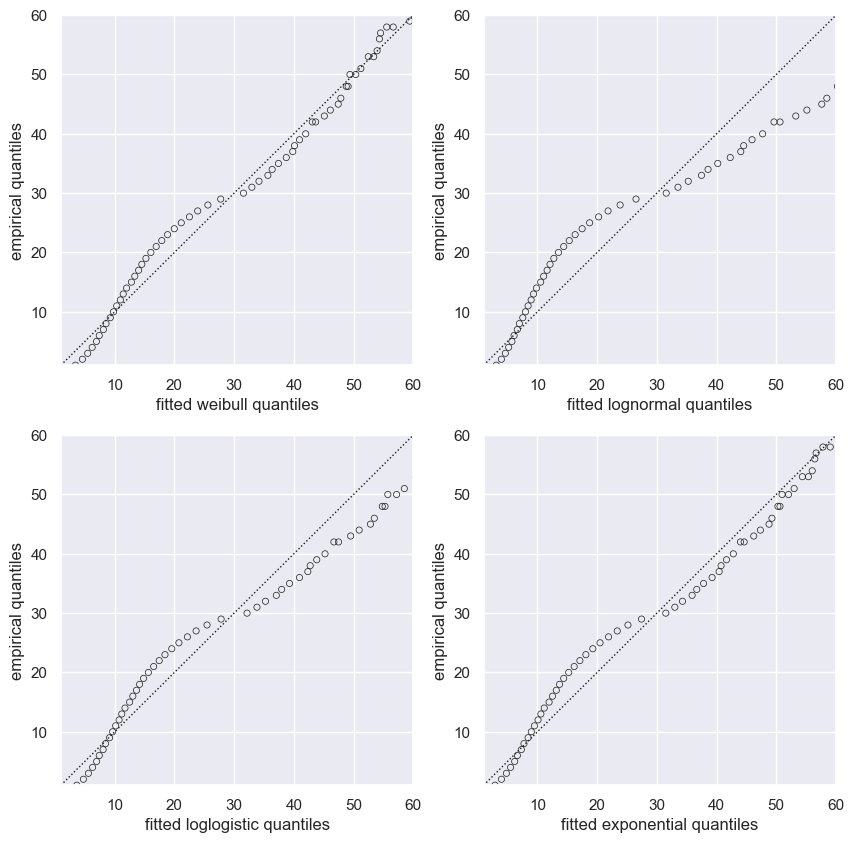
AIC, BIC et QQ Plots#
avec \(k\) le nombre de paramètres (degrés de liberté) du modèle et \(L\) la vraisemblance
avec \(k\) le nombre de paramètres (degrés de liberté) du modèle, \(L\) la vraisemblance et \(N\) le nombre d’observations
1def qq_plots(event_times: pd.Series, event_observed: pd.Series) -> tuple[dict, dict]:
2 fig, axes = plt.subplots(2, 2, figsize=(10, 10))
3 axes = axes.reshape(4)
4
5 aic_dict = {}
6 bic_dict = {}
7
8 for i, model in enumerate(
9 [
10 PiecewiseExponentialFitter([9, 21, 29]),
11 WeibullFitter(),
12 LogNormalFitter(),
13 LogLogisticFitter(),
14 ExponentialFitter(),
15 GeneralizedGammaFitter(),
16 ]
17 ):
18 model.fit(event_times, event_observed)
19
20 if not isinstance(model, PiecewiseExponentialFitter) and not isinstance(
21 model, GeneralizedGammaFitter
22 ):
23 qq_plot(model, ax=axes[i - 1])
24
25 model_name = model.__class__.__name__
26 model_name = model_name.replace("Fitter", "")
27
28 aic_dict[model_name] = model.AIC_
29 bic_dict[model_name] = model.BIC_
30
31 return aic_dict, bic_dict
QQ Plots#
1aic_dict, bic_dict = qq_plots(event_times, event_observed)
AIC et BIC#
1score_dict = {
2 "Modèle": [],
3 "Métrique": [],
4 "Valeur": [],
5}
1for model in aic_dict.keys():
2 score_dict["Modèle"].append(model)
3 score_dict["Métrique"].append("aic")
4 score_dict["Valeur"].append(aic_dict[model])
5
6 score_dict["Modèle"].append(model)
7 score_dict["Métrique"].append("bic")
8 score_dict["Valeur"].append(bic_dict[model])
1df_score = pd.DataFrame(score_dict)
1aic_df = df_score[df_score["Métrique"] == "aic"].sort_values("Valeur")
1bic_df = df_score[df_score["Métrique"] == "bic"].sort_values("Valeur")
1# print(aic_df.to_markdown(index=False))
2# print(bic_df.to_markdown(index=False))
1plt.figure(figsize=(12, 8))
2plt.title("Comparaison des modèles paramétriques")
3sns.barplot(data=score_dict, x="Modèle", y="Valeur", hue="Métrique", width=0.5)
<Axes: title={'center': 'Comparaison des modèles paramétriques'}, xlabel='Modèle', ylabel='Valeur'>
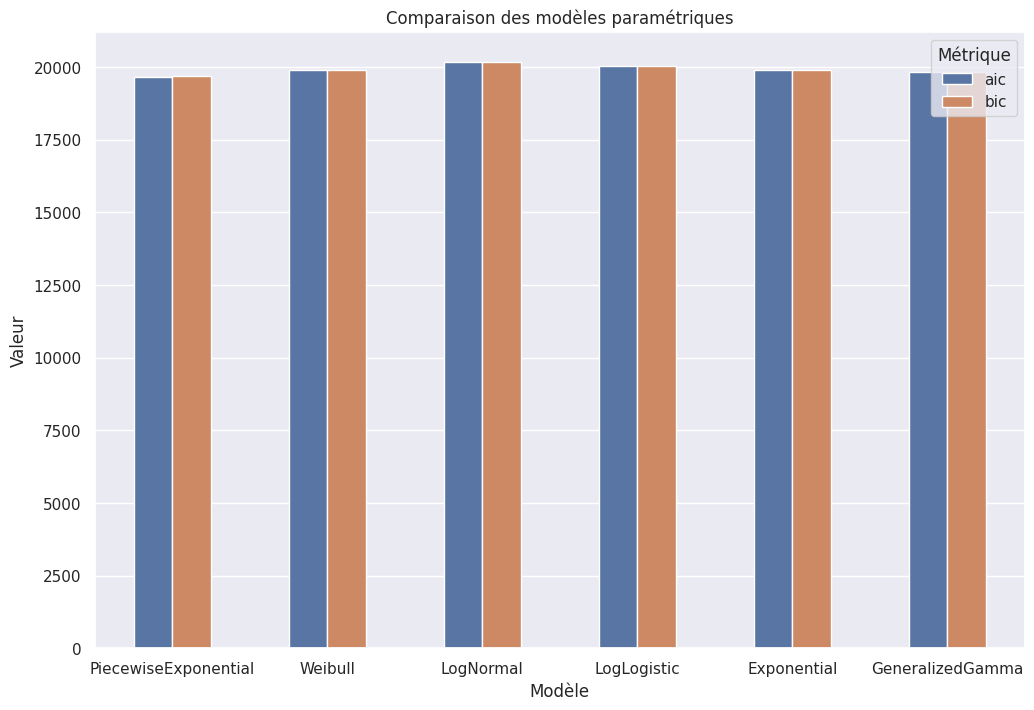
Tableau. AIC des modèles paramétriques (par ordre croissant)
Modèle |
AIC |
|---|---|
PiecewiseExponential |
19651.1 |
GeneralizedGamma |
19818.2 |
Weibull |
19887.7 |
Exponential |
19897.5 |
LogLogistic |
20021.3 |
LogNormal |
20172.2 |
Tableau. BIC des modèles paramétriques (par ordre croissant)
Modèle |
BIC |
|---|---|
PiecewiseExponential |
19676.5 |
GeneralizedGamma |
19837.2 |
Weibull |
19900.4 |
Exponential |
19903.8 |
LogLogistic |
20033.9 |
LogNormal |
20184.9 |
Meilleur modèle paramétrique#
Tableau. Récapitulatif des modèles paramétriques
Modèle |
Test de |
QQ Plot |
AIC |
BIC |
|---|---|---|---|---|
Weibull |
❌ |
✅ |
19887.7 |
19900.4 |
Exponential |
❌ |
✅ |
19897.5 |
19903.8 |
PiecewiseExponential |
❌ |
✅ |
19651.1 |
19676.5 |
LogNormal |
❌ |
❌ |
20172.2 |
20184.9 |
LogLogistic |
❌ |
✅ |
20021.3 |
20033.9 |
Gamma généralisé |
❌ |
❌ |
19818.2 |
19837.2 |
Choix du modèle paramétrique : exponentiel par morceau
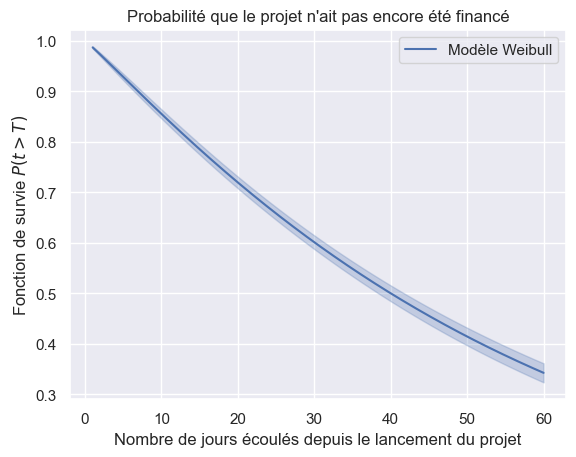
1plot_survival_estimation(km, event_times, event_observed, "Kaplan-Meier")
2best_model.plot_survival_function()
<Axes: title={'center': "Probabilité que le projet n'ait pas encore été financé"}, xlabel='Nombre de jours écoulés depuis le lancement du projet', ylabel='Fonction de survie $P(t > T)$'>
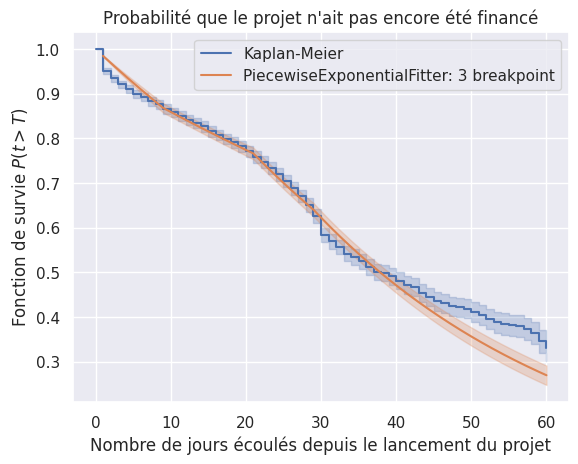
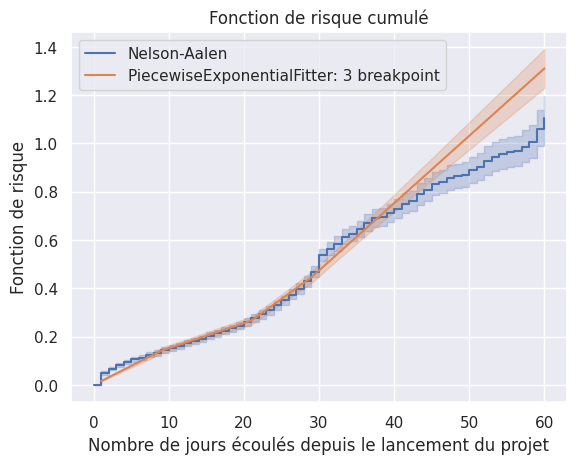
1hazard_models = create_hazard_models()
2
3plot_hazard_estimation(
4 hazard_models["Nelson-Aalen"], event_times, event_observed, "Nelson-Aalen"
5)
6
7best_model.plot_cumulative_hazard()
<Axes: title={'center': 'Fonction de risque cumulé'}, xlabel='Nombre de jours écoulés depuis le lancement du projet', ylabel='Fonction de risque'>
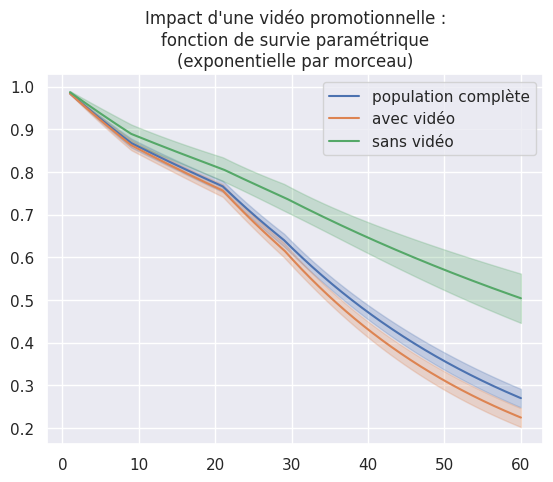
1plt.title(
2 "Impact d'une vidéo promotionnelle :\nfonction de survie paramétrique\n(exponentielle par morceau)"
3)
4
5best_model.fit(event_times, event_observed)
6best_model.plot_survival_function(label="population complète")
7
8best_model.fit(t_video, o_video)
9best_model.plot_survival_function(label="avec vidéo")
10
11best_model.fit(t_no_video, o_no_video)
12best_model.plot_survival_function(label="sans vidéo")
<Axes: title={'center': "Impact d'une vidéo promotionnelle :\nfonction de survie paramétrique\n(exponentielle par morceau)"}>