Régression non-paramétrique

Objectif

• vérifier l’hypothèse de hazard proportionnel

• régression non-paramétrique et paramétrique

• choisir le meilleur modèle pour chaque

Tableau. Notre démarche pour les régressions non-paramétriques.

Régressions non-paramétriques testées	Critère de sélection
- Cox proportionnel	- indice de concordance
- Aalen additif	- MAE de prédiction (cross-validée)
- Aalen additif avec pénalité (hyper-paramètre)

Tableau. Notre démarche pour les régressions paramétriques.

Régressions paramétriques testées	Critère de sélection
- Weibull AFT	- AIC
- Exponentiel par morceaux (3 morceaux)	- BIC
- Exponentiel par morceaux (5 morceaux)	- MAE de prédiction (cross-validée)

import numpy as np
import pandas as pd
from lifelines import *
from lifelines import (
    AalenAdditiveFitter,
    CoxPHFitter,
    LogNormalAFTFitter,
    PiecewiseExponentialRegressionFitter,
    WeibullAFTFitter,
    WeibullFitter,
)
from lifelines.plotting import qq_plot
from lifelines.utils import find_best_parametric_model, k_fold_cross_validation
from matplotlib import pyplot as plt
from sklearn.metrics import mean_absolute_error

from src.utils import init_notebook

init_notebook()

Données

df = pd.read_csv(
    "data/kickstarter_1.csv",
    parse_dates=True,
)

df = df[
    [
        "day_succ",
        "Status",
        "has_video",
        "facebook_connected",
        "goal",
        "facebook_friends",
    ]
]

event_times = df["day_succ"]
event_observed = df["Status"]

cph = CoxPHFitter()
cph.fit(df, duration_col="day_succ", event_col="Status")

<lifelines.CoxPHFitter: fitted with 4175 total observations, 2213 right-censored observations>

Vérification du hazard proportionnel

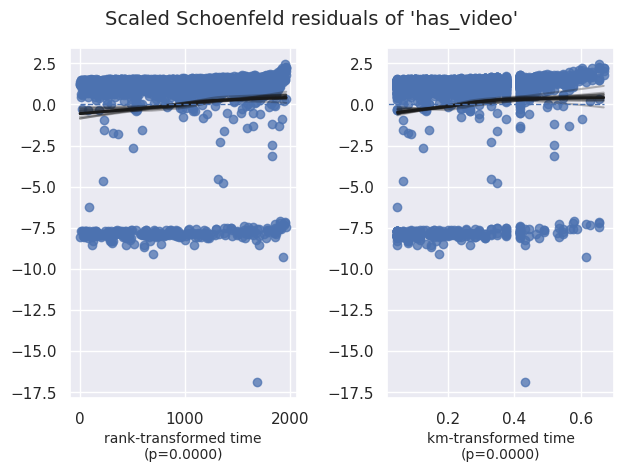
cph.check_assumptions(df, show_plots=True)

   Bootstrapping lowess lines. May take a moment...

The ``p_value_threshold`` is set at 0.01. Even under the null hypothesis of no violations, some
covariates will be below the threshold by chance. This is compounded when there are many covariates.
Similarly, when there are lots of observations, even minor deviances from the proportional hazard
assumption will be flagged.

With that in mind, it's best to use a combination of statistical tests and visual tests to determine
the most serious violations. Produce visual plots using ``check_assumptions(..., show_plots=True)``
and looking for non-constant lines. See link [A] below for a full example.

null_distribution	chi squared
degrees_of_freedom	1
model	<lifelines.CoxPHFitter: fitted with 4175 total...
test_name	proportional_hazard_test

		test_statistic	p	-log2(p)
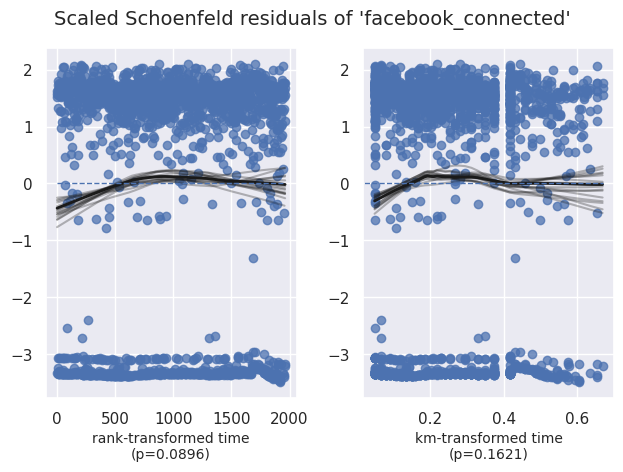
facebook_connected	km	1.95	0.16	2.63
	rank	2.88	0.09	3.48
facebook_friends	km	7.22	0.01	7.12
	rank	5.95	0.01	6.08
goal	km	12.49	<0.005	11.26
	rank	10.95	<0.005	10.06
has_video	km	19.02	<0.005	16.24
	rank	20.93	<0.005	17.68

1. Variable 'has_video' failed the non-proportional test: p-value is <5e-05.

   Advice: with so few unique values (only 2), you can include `strata=['has_video', ...]` in the
call in `.fit`. See documentation in link [E] below.

   Bootstrapping lowess lines. May take a moment...

   Bootstrapping lowess lines. May take a moment...

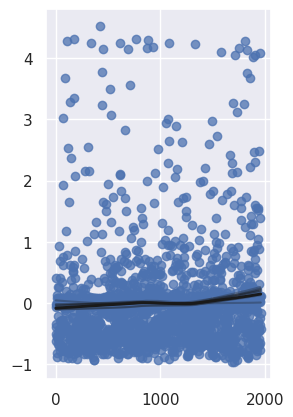
2. Variable 'goal' failed the non-proportional test: p-value is 0.0004.

   Advice 1: the functional form of the variable 'goal' might be incorrect. That is, there may be
non-linear terms missing. The proportional hazard test used is very sensitive to incorrect
functional forms. See documentation in link [D] below on how to specify a functional form.

   Advice 2: try binning the variable 'goal' using pd.cut, and then specify it in `strata=['goal',
...]` in the call in `.fit`. See documentation in link [B] below.

   Advice 3: try adding an interaction term with your time variable. See documentation in link [C]
below.


   Bootstrapping lowess lines. May take a moment...

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[7], line 1
----> 1 cph.check_assumptions(df, show_plots=True)

File ~/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-8mQTRXZa-py3.10/lib/python3.10/site-packages/lifelines/fitters/mixins.py:139, in ProportionalHazardMixin.check_assumptions(self, training_df, advice, show_plots, p_value_threshold, plot_n_bootstraps, columns)
    137     ix = sorted(np.random.choice(n, n))
    138     tt_ = tt.values[ix]
--> 139     y_lowess = lowess(tt_, y.values[ix])
    140     ax.plot(tt_, y_lowess, color="k", alpha=0.30)
    142 best_xlim = ax.get_xlim()

File ~/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-8mQTRXZa-py3.10/lib/python3.10/site-packages/lifelines/utils/lowess.py:49, in lowess(x, y, f, iterations)
     47 for i in range(n):
     48     weights = delta * w[:, i]
---> 49     b = np.array([np.sum(weights * y), np.sum(weights * y * x)])
     50     A = np.array([[np.sum(weights), np.sum(weights * x)], [np.sum(weights * x), np.sum(weights * x * x)]])
     51     # I think it is safe to assume this.
     52     # pylint: disable=unexpected-keyword-arg

File ~/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-8mQTRXZa-py3.10/lib/python3.10/site-packages/numpy/core/fromnumeric.py:2313, in sum(a, axis, dtype, out, keepdims, initial, where)
   2310         return out
   2311     return res
-> 2313 return _wrapreduction(a, np.add, 'sum', axis, dtype, out, keepdims=keepdims,
   2314                       initial=initial, where=where)

File ~/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-8mQTRXZa-py3.10/lib/python3.10/site-packages/numpy/core/fromnumeric.py:88, in _wrapreduction(obj, ufunc, method, axis, dtype, out, **kwargs)
     85         else:
     86             return reduction(axis=axis, out=out, **passkwargs)
---> 88 return ufunc.reduce(obj, axis, dtype, out, **passkwargs)

KeyboardInterrupt: 

Modèles non-paramétrique

Modèle de Cox

cph.print_summary()

model	lifelines.CoxPHFitter
duration col	'day_succ'
event col	'Status'
baseline estimation	breslow
number of observations	3340
number of events observed	1569
partial log-likelihood	-11708.02
time fit was run	2024-01-15 23:19:26 UTC

	coef	exp(coef)	se(coef)	coef lower 95%	coef upper 95%	exp(coef) lower 95%	exp(coef) upper 95%	cmp to	z	p	-log2(p)
has_video	0.77	2.15	0.08	0.61	0.92	1.84	2.51	0.00	9.72	<0.005	71.73
facebook_connected	-0.04	0.96	0.06	-0.15	0.07	0.86	1.08	0.00	-0.64	0.52	0.94
goal	-21.28	0.00	1.74	-24.70	-17.87	0.00	0.00	0.00	-12.21	<0.005	111.42
facebook_friends	0.15	1.16	0.02	0.11	0.20	1.11	1.22	0.00	6.73	<0.005	35.79

Concordance	0.66
Partial AIC	23424.05
log-likelihood ratio test	409.37 on 4 df
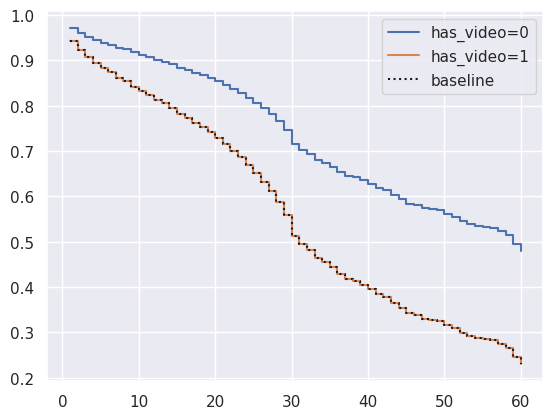
-log2(p) of ll-ratio test	287.61

cph.plot_partial_effects_on_outcome(covariates="has_video", values=[0, 1])

<Axes: >

Cross-validation (Cox & Aalen additif)

# create the three models we'd like to compare.
aaf_1 = AalenAdditiveFitter(coef_penalizer=0)
aaf_2 = AalenAdditiveFitter(coef_penalizer=10)
cph = CoxPHFitter()

def moyenne_cross_val(model, df: pd.DataFrame):
    return np.mean(
        k_fold_cross_validation(
            model,
            df,
            duration_col="day_succ",
            event_col="Status",
            scoring_method="concordance_index",
        )
    )

models_list = {
    "Cox proportionnel": cph,
    "Aalen Additive (sans pénalité)": aaf_1,
    "Aalen Additive (pénalité 10)": aaf_2,
}

cox_tab = {
    "Modèle": [],
    "Indice de concordance": [],
}  # todo: rename

for model in models_list.keys():
    m = models_list[model]
    moy = moyenne_cross_val(m, df)

    cox_tab["Modèle"].append(model)
    cox_tab["Indice de concordance"].append(moy)

# print(pd.DataFrame(cox_tab).to_markdown(index=False))

Tableau. Comparaison des modèles de régression non-paramétriques.

Modèle	Indice de concordance
Cox proportionnel	0.656568
Aalen Additive (sans pénalité)	0.586883
Aalen Additive (pénalité 10)	0.588575

Interprétation :

• indice de concordance > 0.5 => performance supérieure à du hasard

• indice de concordance = 0.5 => performance équivalente à du hasard

• indice de concordance < 0.5 => performance inférieure à du hasard

Choix : modèle de Cox proportionnel

Prédictions

models_nonparam = {
    "Cox proportionnel": cph,
    "Aalen additif (sans pénalité)": aaf_1,
    "Aalen additif (avec pénalité=10)": aaf_2,
}

models_param = {
    "Weibull AFT": WeibullAFTFitter(),
    "Exponentiel morceaux (3)": PiecewiseExponentialRegressionFitter(
        breakpoints=[9, 21, 29]
    ),
    "Exponentiel morceaux (5)": PiecewiseExponentialRegressionFitter(
        breakpoints=[10, 20, 30, 40, 50]
    ),
}

res_models = {
    "Modèle": [],
    "AIC": [],
    "BIC": [],
    "MAE": [],
}

for model_name in models_nonparam.keys():
    model = models_nonparam[model_name]
    model.fit(df, duration_col="day_succ", event_col="Status")

    y_pred = model.predict_expectation(df)
    mae = mean_absolute_error(event_times, y_pred)

    res_models["Modèle"].append(model_name)
    res_models["MAE"].append(mae)
    res_models["AIC"].append(np.nan)
    res_models["BIC"].append(np.nan)

for model_name in models_param.keys():
    model = models_param[model_name]
    model.fit(df, duration_col="day_succ", event_col="Status")

    y_pred = model.predict_expectation(df)
    mae = mean_absolute_error(event_times, y_pred)

    res_models["Modèle"].append(model_name)
    res_models["MAE"].append(mae)
    res_models["AIC"].append(model.AIC_)
    res_models["BIC"].append(model.BIC_)

/home/ab2/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-ue2DmfIx-py3.10/lib/python3.10/site-packages/lifelines/fitters/__init__.py:2371: ApproximationWarning: Approximating using `predict_survival_function`. To increase accuracy, try using or increasing the resolution of the timeline kwarg in `.fit(..., timeline=timeline)`.

  warnings.warn(
/home/ab2/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-ue2DmfIx-py3.10/lib/python3.10/site-packages/lifelines/fitters/__init__.py:2507: ApproximationWarning: Approximating the expected value using trapezoid rule.

  warnings.warn("""Approximating the expected value using trapezoid rule.\n""", exceptions.ApproximationWarning)
/home/ab2/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-ue2DmfIx-py3.10/lib/python3.10/site-packages/lifelines/fitters/__init__.py:2371: ApproximationWarning: Approximating using `predict_survival_function`. To increase accuracy, try using or increasing the resolution of the timeline kwarg in `.fit(..., timeline=timeline)`.

  warnings.warn(
/home/ab2/.cache/pypoetry/virtualenvs/kickstarter-project-analysis-ue2DmfIx-py3.10/lib/python3.10/site-packages/lifelines/fitters/__init__.py:2507: ApproximationWarning: Approximating the expected value using trapezoid rule.

  warnings.warn("""Approximating the expected value using trapezoid rule.\n""", exceptions.ApproximationWarning)

# print(pd.DataFrame(res_models).to_markdown(index=False))

Tableau. Résultats des modèles de régression

Modèle	AIC	BIC	MAE
Cox proportionnel	nan	nan	13.6055
Aalen additif (sans pénalité)	nan	nan	13.9461
Aalen additif (avec pénalité=10)	nan	nan	14.0145
Weibull AFT	19465.7	19470.3	3.24738e+77
Exponentiel morceaux (3)	19127.7	19121.1	13.0742
Exponentiel morceaux (5)	19138.1	19128.1	13.2367

Meilleur modèle : exponentiel par morceaux (3)

Nos 3 meilleurs modèles de régression sont :

1. Exponenentiel morceaux (3)

2. Exponentiel morceaux (5)

3. Cox proportionnel