Lois de reproduction choisies

import matplotlib.pyplot as plt
from src.code.simulation.probability_distributions import (
    create_distributions,
    create_distributions_df,
    plot_distribution,
)
from src.config.config import seed
from src.utils.utils import init_notebook

init_notebook(seed)

Résumé des lois

distributions = create_distributions()

df_distribution = create_distributions_df()
df_distribution

	Loi de reproduction	Espérance	Variance	Lambda théorique loi exponentielle Z_n / n
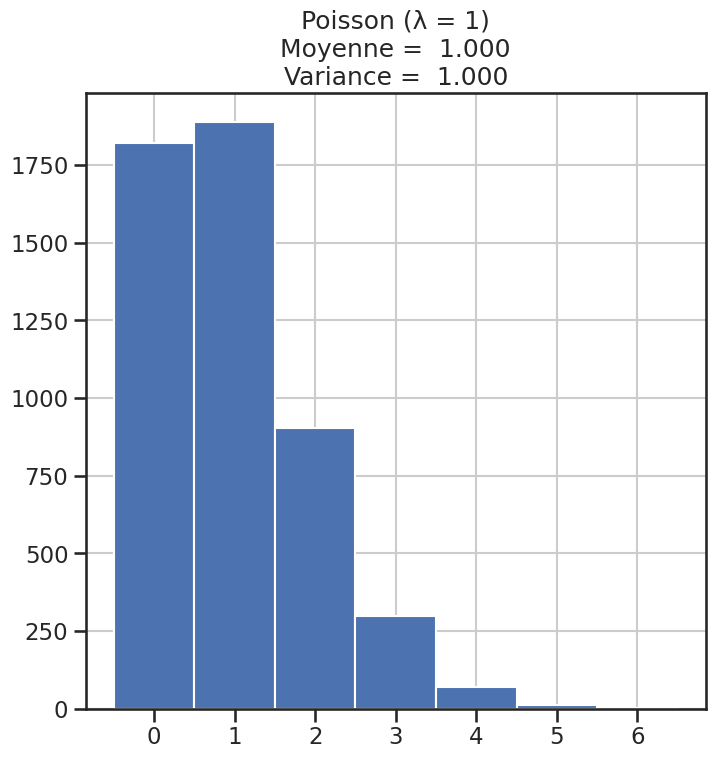
0	Poisson (λ = 1)	1	1.00000	2.000000
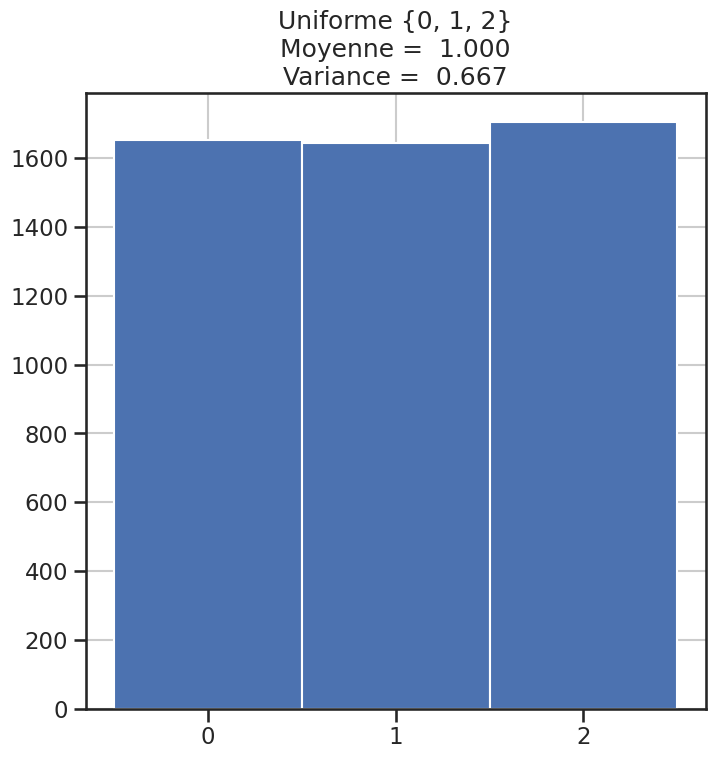
1	Uniforme {0, 1, 2}	1	0.66667	3.000000
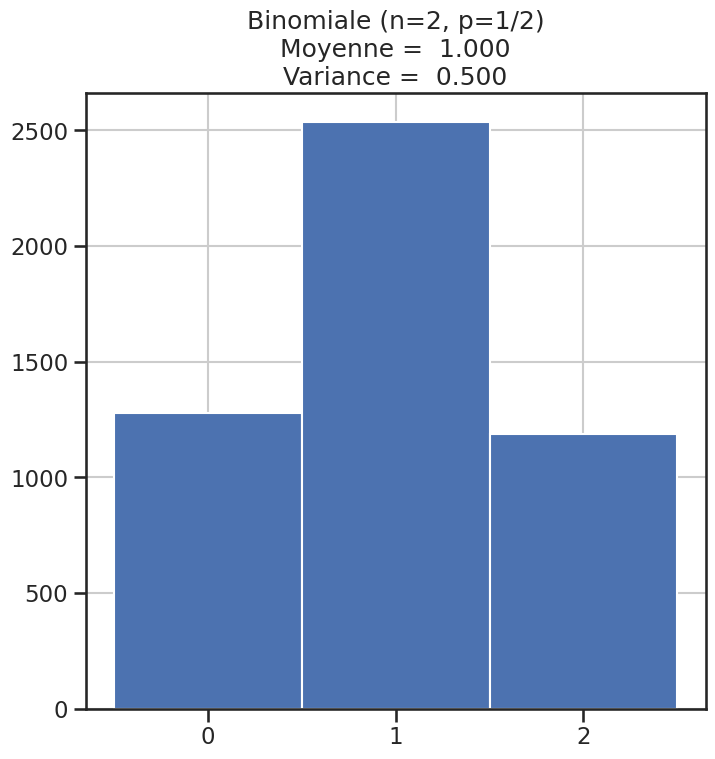
2	Binomiale (n=2, p=1/2)	1	0.50000	4.000000
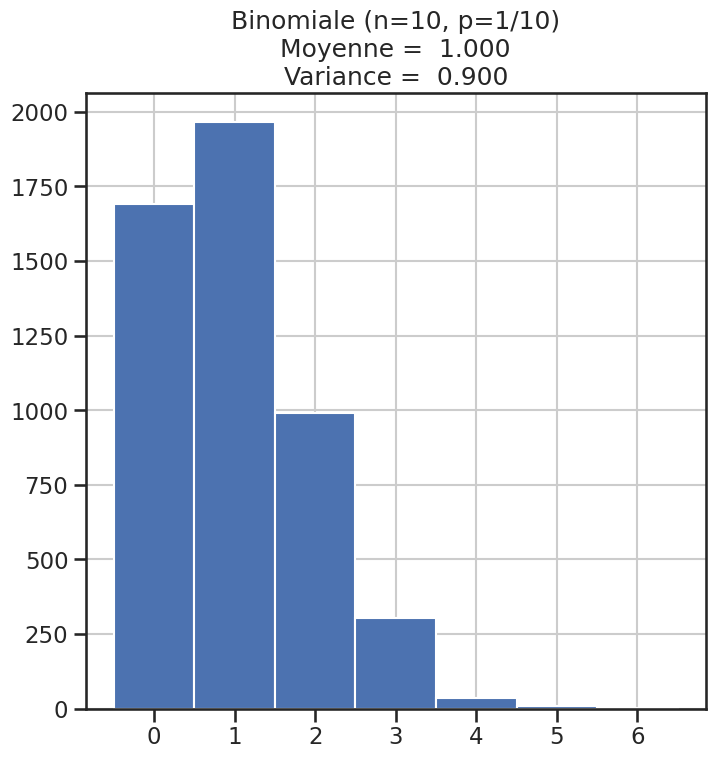
3	Binomiale (n=10, p=1/10)	1	0.90000	2.222222
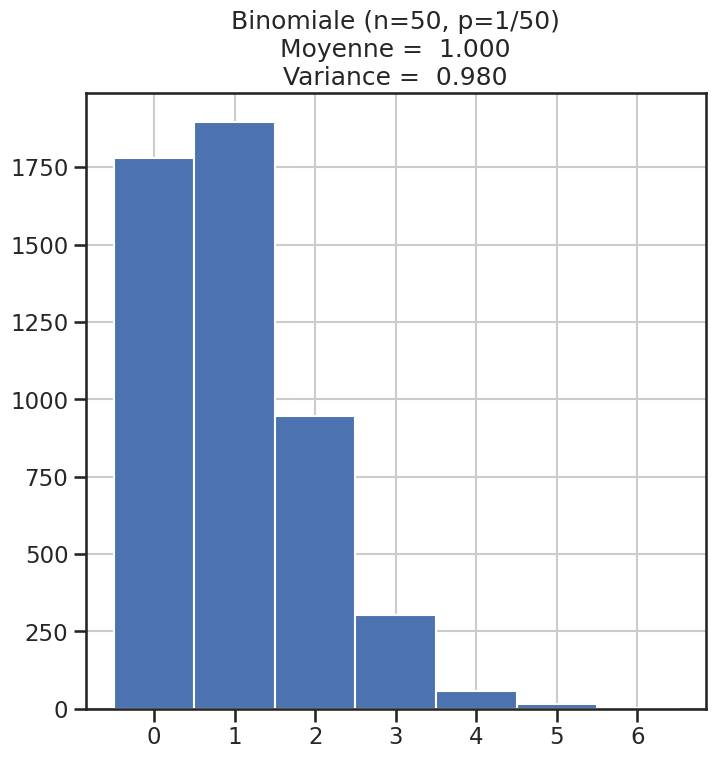
4	Binomiale (n=50, p=1/50)	1	0.98000	2.040816
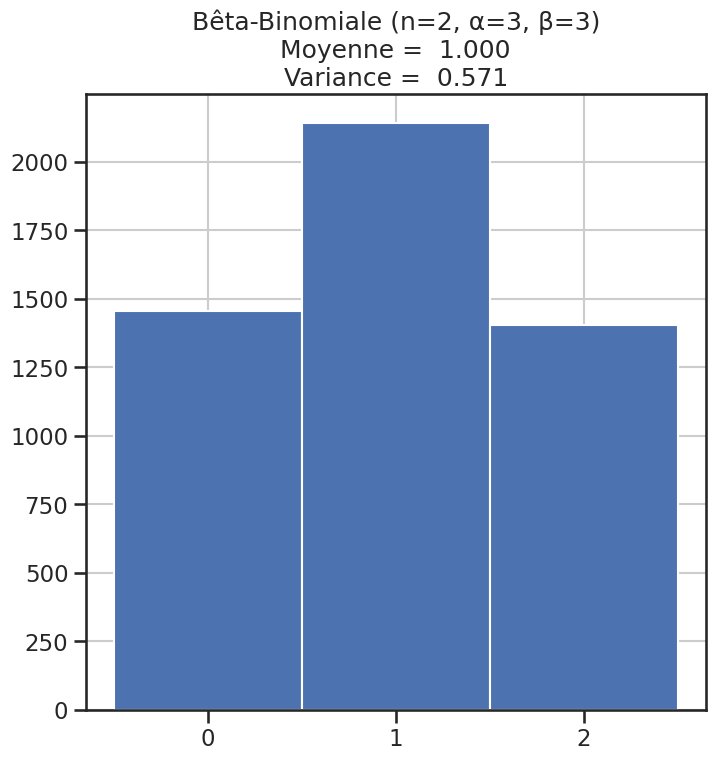
5	Bêta-Binomiale (n=2, α=3, β=3)	1	0.57143	3.500000
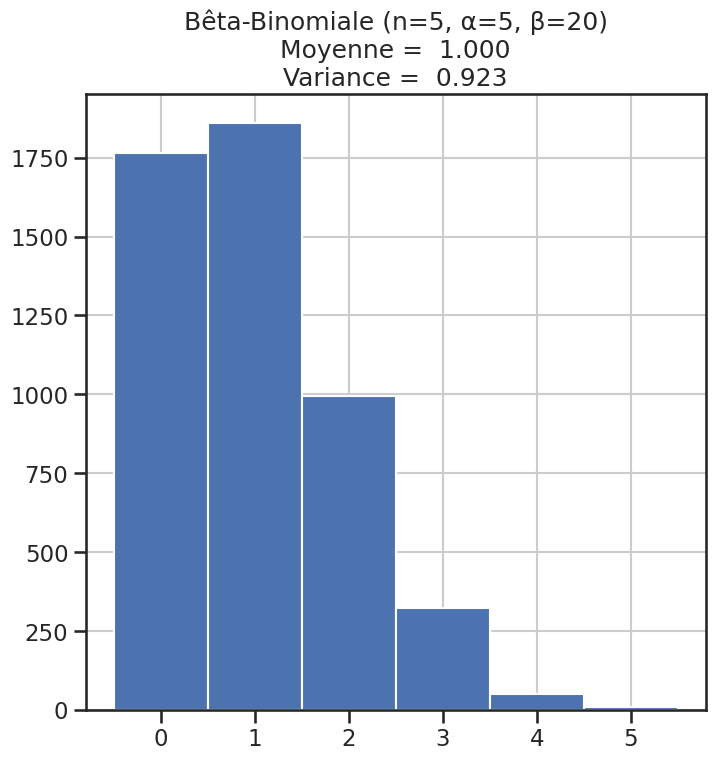
6	Bêta-Binomiale (n=5, α=5, β=20)	1	0.92308	2.166667
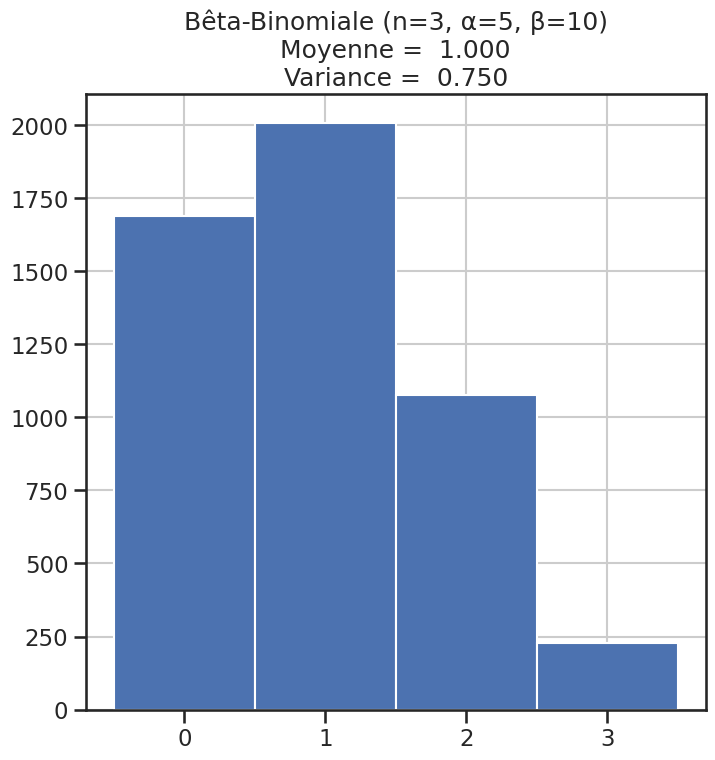
7	Bêta-Binomiale (n=3, α=5, β=10)	1	0.75000	2.666667
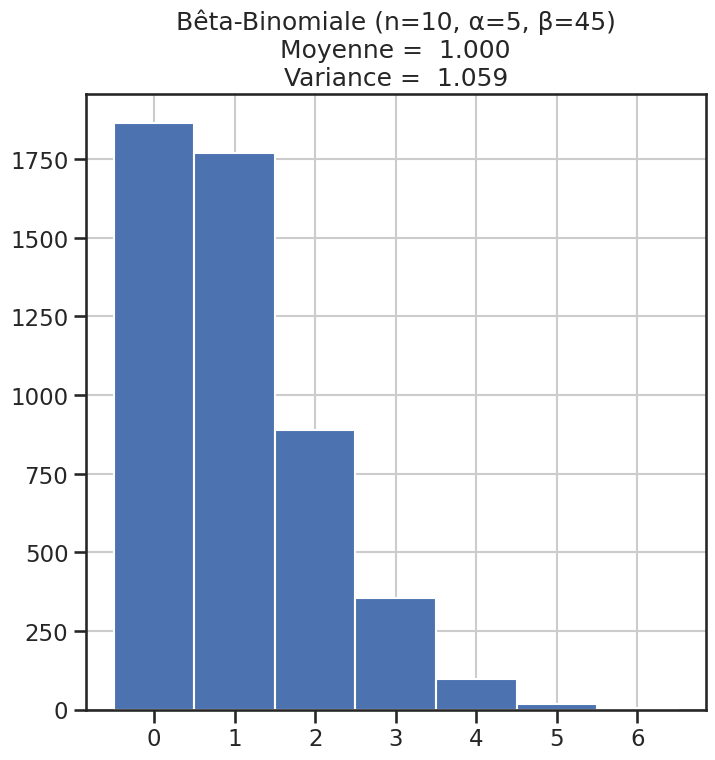
8	Bêta-Binomiale (n=10, α=5, β=45)	1	1.05882	1.888889
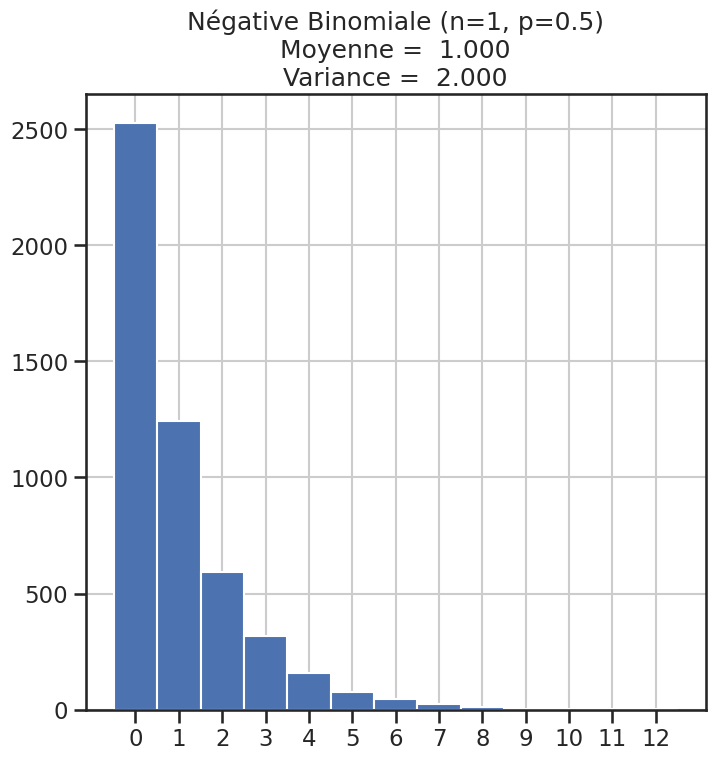
9	Négative Binomiale (n=1, p=0.5)	1	2.00000	1.000000
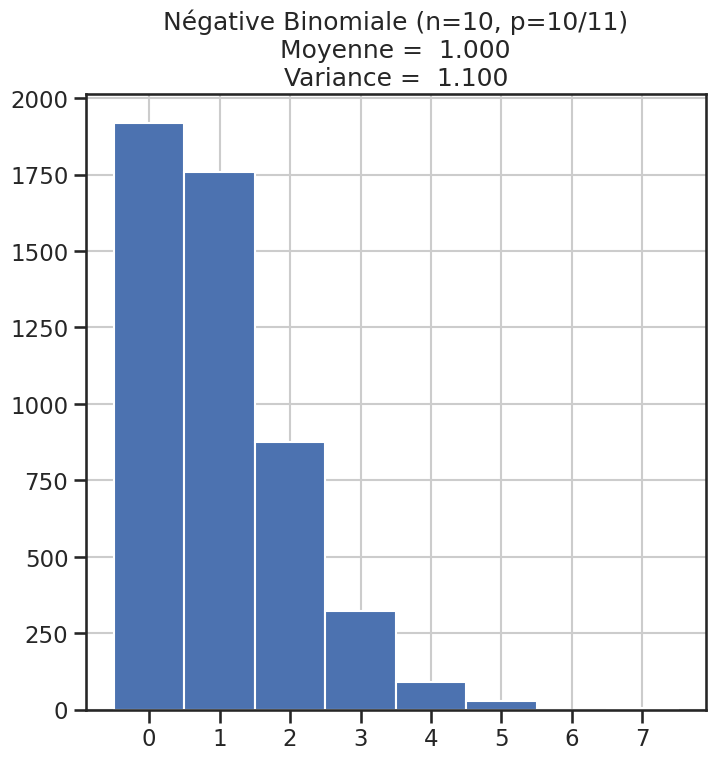
10	Négative Binomiale (n=10, p=10/11)	1	1.10000	1.818182
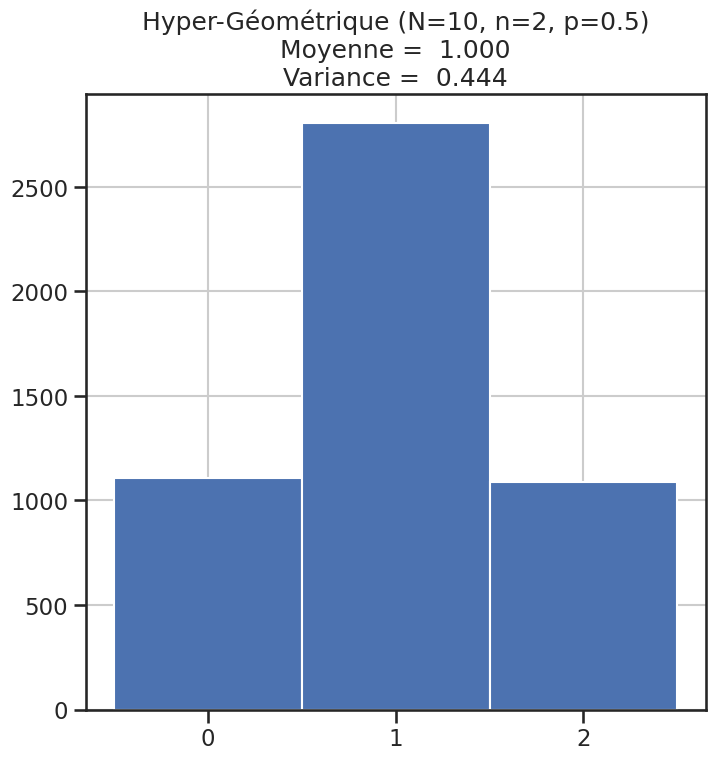
11	Hyper-Géométrique (N=10, n=2, p=0.5)	1	0.44444	4.500000
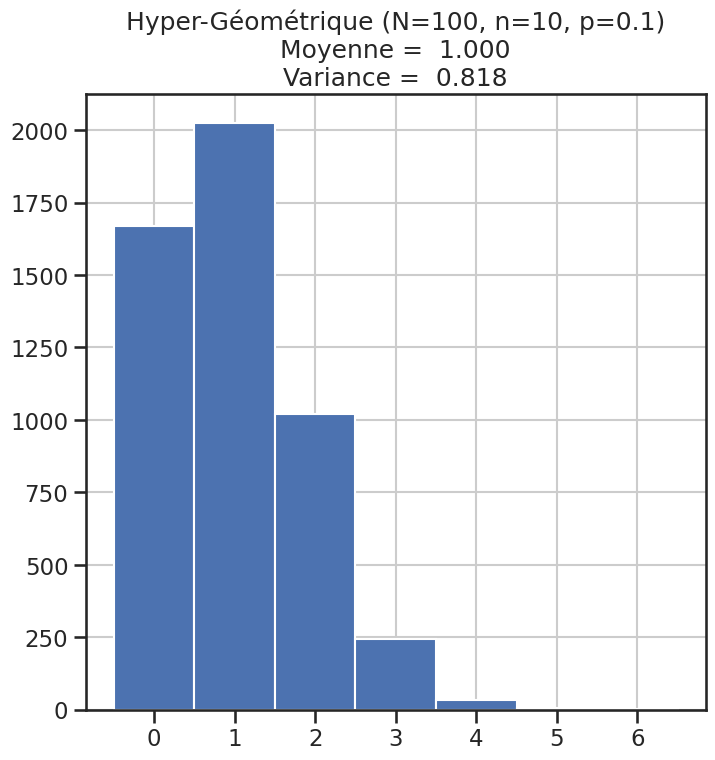
12	Hyper-Géométrique (N=100, n=10, p=0.1)	1	0.81818	2.444444

df_distribution.to_csv("data/distributions.csv", index=False)

Histogramme des lois

for name, distribution in distributions.items():
    plt.figure(figsize=(8, 8))
    plt.title(
        f"{name}\nMoyenne = {distribution.mean() : .3f}\nVariance = {distribution.var() : .3f}",
    )
    plot_distribution(distribution)

    filename = name.replace("=", "").replace("/", "")
    plt.savefig(f"data/plots/distribution/histogram/{filename}.png")

    plt.show()